题目内容
 如图,在四边形ABCD中,
如图,在四边形ABCD中, R),
R), ,
, ,且△BCD是以BC为斜边的直角三角形.求:
,且△BCD是以BC为斜边的直角三角形.求:
(1)λ的值;
(2) 的值.
的值.
(1)因为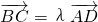 ,所以BC∥AD,且
,所以BC∥AD,且 .
.
因为 ,所以
,所以 .
.
又 ,所以
,所以 .
.
作AH⊥BD于H,则H为BD的中点.
在Rt△AHB中,得 ,于是∠ABH=30°.
,于是∠ABH=30°.
所以∠ADB=∠DBC=30°.
而∠BDC=90°,所以BD=BCcos30°,即 ,解得λ=2.
,解得λ=2.
(2)由(1)知,∠ABC=60°,|
所以 与
与 的夹角为120°.
的夹角为120°.
故 .
.
分析:(1)由题意可知 且△ABD是三边分别为2,2,
且△ABD是三边分别为2,2, 的等腰三角形,利用已知条件可得∠ABD=30°,从而可得∠ABD=∠ADB=∠DBC=30°,解直角三角形可得λ
的等腰三角形,利用已知条件可得∠ABD=30°,从而可得∠ABD=∠ADB=∠DBC=30°,解直角三角形可得λ
(2)由(1)知,∠ABC=60°,| |=4,从而可得
|=4,从而可得 的夹角1200,代入向量的数量积公式,即可.
的夹角1200,代入向量的数量积公式,即可.
点评:本题考查了平面向量共线的条件,向量减法的平行四边形法则,平面向量的夹角及数量积的定义,要注意求两向量的夹角时,一定要保证两向量共起点,避免夹角的求解错误.
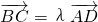 ,所以BC∥AD,且
,所以BC∥AD,且 .
.因为
 ,所以
,所以 .
.又
 ,所以
,所以 .
.作AH⊥BD于H,则H为BD的中点.
在Rt△AHB中,得
 ,于是∠ABH=30°.
,于是∠ABH=30°.所以∠ADB=∠DBC=30°.
而∠BDC=90°,所以BD=BCcos30°,即
 ,解得λ=2.
,解得λ=2.(2)由(1)知,∠ABC=60°,|

所以
 与
与 的夹角为120°.
的夹角为120°.故
 .
.分析:(1)由题意可知
 且△ABD是三边分别为2,2,
且△ABD是三边分别为2,2, 的等腰三角形,利用已知条件可得∠ABD=30°,从而可得∠ABD=∠ADB=∠DBC=30°,解直角三角形可得λ
的等腰三角形,利用已知条件可得∠ABD=30°,从而可得∠ABD=∠ADB=∠DBC=30°,解直角三角形可得λ(2)由(1)知,∠ABC=60°,|
 |=4,从而可得
|=4,从而可得 的夹角1200,代入向量的数量积公式,即可.
的夹角1200,代入向量的数量积公式,即可.点评:本题考查了平面向量共线的条件,向量减法的平行四边形法则,平面向量的夹角及数量积的定义,要注意求两向量的夹角时,一定要保证两向量共起点,避免夹角的求解错误.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,在四边形ABCD中,△ABC为边长等于
如图,在四边形ABCD中,△ABC为边长等于 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=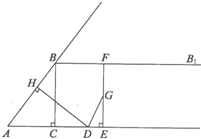 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,