题目内容
设f(θ)=cos2θ+2msinθ-2m-2.若f(θ)<0在θ∈[0,
]上恒成立,求m的取值范围.
| π | 2 |
分析:构造函数f(θ)=cos2θ+2msinθ-2m-2,利用同角三角形函数关系,可将函数的解析式化为f(θ)=-(sinθ-m)2+m2-2m-1的形式,分-1≤m≤1,m≥1,m≤-1三种情况,讨论函数的最大值,最后汇总讨论结果,即可得到答案.
解答:解:设f(θ)=cos2θ+2msinθ-2m-2,
要使f(θ)<0对θ∈[0,
]总成立,当且仅当函数y=f(θ)的最大值小于零.
f(θ)=cos2θ+2msinθ-2m-2=1-sin2θ+2msinθ-2m-2=-(sinθ-m)2+m2-2m-1,
令t=sinθ∈[0,1],g(t)=-(t-m)2+m2-2m-1
∴当0≤m≤1时,函数的最大值为m2-2m-1<0,解得0≤m≤1;
当m>1时,函数的最大值为g(1)<0,得m>1.
∴m≥1时均成立;
当m<0时,函数的最大值为g(0)=-4m-2<0,m>-
.
综上得m的取值范围是m∈(-
,+∞).
要使f(θ)<0对θ∈[0,
| π |
| 2 |
f(θ)=cos2θ+2msinθ-2m-2=1-sin2θ+2msinθ-2m-2=-(sinθ-m)2+m2-2m-1,
令t=sinθ∈[0,1],g(t)=-(t-m)2+m2-2m-1
∴当0≤m≤1时,函数的最大值为m2-2m-1<0,解得0≤m≤1;
当m>1时,函数的最大值为g(1)<0,得m>1.
∴m≥1时均成立;
当m<0时,函数的最大值为g(0)=-4m-2<0,m>-
| 1 |
| 2 |
综上得m的取值范围是m∈(-
| 1 |
| 2 |
点评:本题考查的知识点是三角函数的最值,其中构造函数f(θ)=cos2θ+2msinθ-2m-2,将问题转化为函数恒成立问题是解答本题的关键.

练习册系列答案
相关题目
 sinωxcosωx
sinωxcosωx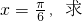 ω的值.
ω的值. sinωxcosωx
sinωxcosωx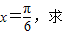 ω的值.
ω的值.