题目内容
1．
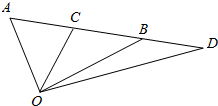如图，已知$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$，$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$，试用$\overrightarrow{OA}$，$\overrightarrow{OB}$表示$\overrightarrow{OC}$和$\overrightarrow{OD}$．
分析 根据向量减法的几何意义，$\overrightarrow{AC}$变成$\overrightarrow{OC}-\overrightarrow{OA}$，$\overrightarrow{AB}$变成$\overrightarrow{OB}-\overrightarrow{OA}$，以及$\overrightarrow{AD}$变成$\overrightarrow{OD}-\overrightarrow{OA}$，带入，并进行向量的数乘运算即可．
解答 解：$\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}$；
∴$\overrightarrow{OC}-\overrightarrow{OA}=\frac{1}{2}（\overrightarrow{OB}-\overrightarrow{OA}）$；
∴$\overrightarrow{OC}=\frac{1}{2}（\overrightarrow{OA}+\overrightarrow{OB}）$；
$\overrightarrow{AD}=\frac{3}{2}\overrightarrow{AB}$；
∴$\overrightarrow{OD}-\overrightarrow{OA}=\frac{3}{2}（\overrightarrow{OB}-\overrightarrow{OA}）$；
∴$\overrightarrow{OD}=-\frac{1}{2}\overrightarrow{OA}+\frac{3}{2}\overrightarrow{OB}$．
点评 考查向量减法的几何意义，以及向量的数乘运算．
练习册系列答案
相关题目
11．函数y=$\frac{1}{\sqrt{x-{x}^{2}}}$的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | 4 |
9．两个变量y与x的回归模型中，分别选择了4个不同模型，计算出它们的相关指数R2如下，其中拟合效果最好的模型是（ ）
| A． | 模型1（相关指数2为0.97） | B． | 模型2（相关指数R2为0.89） | ||
| C． | 模型3（相关指数R2为0.56 ） | D． | 模型4（相关指数R2为0.45） |