题目内容
13.已知函数f(x)=ln(-$\frac{1}{x}$)+$\frac{x+a}{x}$(a∈R)(1)讨论函数f(x)的单调性
(2)函数y=h(x)与函数y=f(x)的图象关于原点对称且h(1)=0,就函数y分别求下面两问:
(I)问是否存在过点(1,-1)的直线与函数y=h(x)的图象相切?若存在,有几条直线,若不存在,说明理由
(Ⅱ)求证:对下任意正整数n.均有1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$≥ln$\frac{{e}^{n}}{n!}$(e为自然对数).
分析 (1)先对函数求导,分a>0,a≤0讨论函数的定义域及单调区间.
(2)先求出h(x)的表达式,
(II)假设存在满足条件的直线与函数相切,根据导数的几何意义,求出切线方程,结合导数的知识推导.
由(2)知函数h(x)的定义域(0,+∞),在(0,1)是减函数,[1,+∞)是增函数,从而有h(x)≥h(1)⇒$\frac{1}{x}≥ln\frac{e}{x}$,分别把x=1,2,3…代入不等式相加可证.
解答 解:(1)由$\left\{\begin{array}{l}{-\frac{1}{x}>0}\\{x≠0}\end{array}\right.$得x<0,即函数的定义域为(-∞,0),
f(x)=ln(-$\frac{1}{x}$)+$\frac{x+a}{x}$=ln(-$\frac{1}{x}$)+1+$\frac{a}{x}$,
函数的导数f′(x)=$\frac{1}{-\frac{1}{x}}$•$\frac{1}{{x}^{2}}$$-\frac{a}{{x}^{2}}$=-$\frac{1}{x}$$-\frac{a}{{x}^{2}}$=$\frac{-x-a}{{x}^{2}}$,
若a≤0,则f′(x)≥0,即函数单调递增,
若a>0,由f′(x)>0得-x-a>0,得x<-a,此时函数单调递增,
由f′(x)<0得,-x-a<0,得-a<x<0,此时函数单调递减.
(2)(I)∵y=h(x)与函数y=f(x)的图象关于原点对称,
∴-y=ln($\frac{1}{x}$)+$\frac{-x+a}{-x}$=ln$\frac{1}{x}$+$\frac{x-a}{x}$=ln$\frac{1}{x}$+1-$\frac{a}{x}$,
则y=-ln$\frac{1}{x}$-1+$\frac{a}{x}$,(x>0)
即h(x)=-ln$\frac{1}{x}$-1+$\frac{a}{x}$,(x>0).
∵h(1)=0,
∴h(1)=-ln1-1+a=a-1=0,
a=1,
即h(x)=-ln$\frac{1}{x}$-1+$\frac{1}{x}$=lnx+$\frac{1}{x}$-1,(x>0).
h′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$,
假设存在这样的切线,设其中一个切点$T({x_0},ln{x_0}-\frac{{{x_0}-1}}{x_0})$,
切线方程:$y+1=\frac{{{x_0}-1}}{{{x_0}^2}}(x-1)$,将点T坐标代入得:$ln{x_0}-\frac{{{x_0}-1}}{x_0}+1=\frac{{{{({x_0}-1)}^2}}}{{{x_0}^2}}$,
即$ln{x_0}+\frac{3}{x_0}-\frac{1}{{{x_0}^2}}-1=0$,①
设$g(x)=lnx+\frac{3}{x}-\frac{1}{x^2}-1$,则$g'(x)=\frac{(x-1)(x-2)}{x^3}$.
∵x>0,
∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,
故g(x)极大值=g(1)=1>0,g(x)极小值=g(2)=ln2+$\frac{1}{4}$>0.
又$g(\frac{1}{4})=ln\frac{1}{4}$+12-16-1=-ln4-3<0,
注意到g(x)在其定义域上的单调性,知g(x)=0仅在$(\frac{1}{4},1)$内有且仅有一根
所以方程①有且仅有一解,故符合条件的切线有且仅有一条.
(Ⅱ)取a=1,由(1)知$f(x)=lnx-\frac{x-1}{x}≥f(1)=0$,
故$\frac{1}{x}≥1-lnx=ln\frac{e}{x}$,
取x=1,2,3,
则$1+\frac{1}{2}+\frac{1}{3}++\frac{1}{n}≥ln\frac{{e}^{n}}{n!}$.
点评 本题考查了导数的应用:利用导数研究函数单调区间及求最值问题,而对不等式的证明问题,主要是结合函数的单调性,对于存在性问题,通常是先假设存在,由假设出发进行推导,若推出矛盾,说明假设错误,即不存在,反之说明存在.

| A. | 非奇非偶函数 | B. | 既奇又偶函数 | C. | 奇函数 | D. | 偶函数 |
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
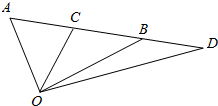 如图,已知$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$,试用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示$\overrightarrow{OC}$和$\overrightarrow{OD}$.
如图,已知$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{AB}$,$\overrightarrow{AD}$=$\frac{3}{2}$$\overrightarrow{AB}$,试用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示$\overrightarrow{OC}$和$\overrightarrow{OD}$.