题目内容
已知数列 中,
中, ,
, ,记
,记 为
为 的前
的前 项的和,
项的和, ,
, .
.
(1)判断数列 是否为等比数列,并求出
是否为等比数列,并求出 ;
;
(2)求 .
.
(1) 是公比为
是公比为 的等比数列,
的等比数列, ;
;
(2)
 .
.
解析试题分析:(1)根据已知条件,注意研究 ,做出准确判断;
,做出准确判断;
由 ,
, ,得到
,得到 ;
;
(2)由(1)可知 ,明确
,明确 是以
是以 为首项,以
为首项,以 为公比的等比数列;
为公比的等比数列; 是以
是以 为首项,以
为首项,以 为公比的等比数列,应用“分组求和法”,计算等比数列的和。
为公比的等比数列,应用“分组求和法”,计算等比数列的和。
解得本题的关键是确定数列的基本特征.
试题解析:(1)
 ,
, ,
, ,即
,即 2分
2分 ,
,

所以 是公比为
是公比为 的等比数列. 5分
的等比数列. 5分 ,
, ,
,

 6分
6分
(2)由(1)可知 ,所以
,所以 是以
是以 为首项,以
为首项,以 为公比的等比数列;
为公比的等比数列; 是以
是以 为首项,以
为首项,以 为公比的等比数列 10分
为公比的等比数列 10分
 12分
12分
考点:等比数列的通项公式及其求和公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的首项
的首项 ,
, ,
, ,
, 为等比数列;
为等比数列; ,求最大的正整数
,求最大的正整数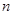 .
. ,n∈N*,且a1=2.
,n∈N*,且a1=2. +
+ +…+
+…+ +
+ ≤n﹣
≤n﹣ (n∈N*)
(n∈N*) 成等比数列, 公比为
成等比数列, 公比为 , 求证:
, 求证: .
. 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数. 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由; 的前
的前 项和为
项和为 ,且
,且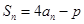 ,其中
,其中 是不为零的常数.
是不为零的常数. 时,数列
时,数列 满足
满足 ,
, ,求数列
,求数列 的各项均满足
的各项均满足 ,
, ,
,

 的通项公式是
的通项公式是 ,前
,前 项和为
项和为 ,求证:对于任意的正数
,求证:对于任意的正数 .
.