题目内容
(14分)(2011•天津)已知数列{an}与{bn}满足bn+1an+bnan+1=(﹣2)n+1,bn= ,n∈N*,且a1=2.
,n∈N*,且a1=2.
(Ⅰ)求a2,a3的值
(Ⅱ)设cn=a2n+1﹣a2n﹣1,n∈N*,证明{cn}是等比数列
(Ⅲ)设Sn为{an}的前n项和,证明 +
+ +…+
+…+ +
+ ≤n﹣
≤n﹣ (n∈N*)
(n∈N*)
(Ⅰ)a2=﹣ a3=8(Ⅱ)(Ⅲ)见解析
a3=8(Ⅱ)(Ⅲ)见解析
解析试题分析:(Ⅰ)推出bn的表达式,分别当n=1时,求出a2=﹣ ;当n=2时,解出a3=8;
;当n=2时,解出a3=8;
(Ⅱ)设cn=a2n+1﹣a2n﹣1,n∈N*,利用等比数列的定义,证明{cn}是等比数列;
(Ⅲ)求出S2n,a2n,S2n﹣1,a2n﹣1,求出 +
+ 的表达式,然后求出
的表达式,然后求出 +
+ +…+
+…+ +
+ 的表达式,利用放缩法证明结果.
的表达式,利用放缩法证明结果.
(Ⅰ)解:由bn= ,(n∈N*)可得bn=
,(n∈N*)可得bn=
又bn+1an+bnan+1=(﹣2)n+1,
当n=1时,a1+2a2=﹣1,可得由a1=2,a2=﹣ ;
;
当n=2时,2a2+a3=5可得a3=8;
(Ⅱ)证明:对任意n∈N*,a2n﹣1+2a2n=﹣22n﹣1+1…①
2a2n+a2n+1=22n+1…②
②﹣①,得a2n+1﹣a2n﹣1=3×22n﹣1,即:cn=3×22n﹣1,于是
所以{cn}是等比数列.
(Ⅲ)证明:
a1=2,由(Ⅱ)知,当k∈N*且k≥2时,
a2k﹣1=a1+(a3﹣a1)+(a5﹣a3)+(a7﹣a5)+…+(a2k﹣1﹣a2k﹣3)
=2+3(2+23+25+…+22k﹣3)=2+3× =22k﹣1,
=22k﹣1,
故对任意的k∈N*,a2k﹣1=22k﹣1.
由①得22k﹣1+2a2k=﹣22k﹣1+1,所以 k∈N*,
k∈N*,
因此,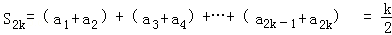
于是, .
.
故 =
=
=
所以,对任意的n∈N*, +
+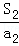 +…+
+…+ +
+ =(
=( +
+ )+…+(
)+…+( +
+ )
)
=
=
=n﹣
≤n﹣ ﹣
﹣ =n﹣
=n﹣ (n∈N*)
(n∈N*)
点评:本题考查等比数列的定义,等比数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力以及分类讨论思想.

 的首项
的首项 ,且
,且
 .
. 的前
的前 项和
项和 .
. 中,已知
中,已知 ,
, ,
, .
.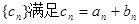 ,求
,求 的前
的前 项和
项和 .
. }中,
}中,
 }是等比数列,并求出数列{
}是等比数列,并求出数列{ 中,
中, ,
, ,记
,记 为
为 项的和,
项的和, ,
, .
. 是否为等比数列,并求出
是否为等比数列,并求出 ;
;  ,其前
,其前 项和
项和 满足
满足 且
且 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; 表示不超过实数
表示不超过实数 的最大整数,记
的最大整数,记 ,求
,求 .
.