题目内容
(本题满分10分)已知数列 的首项
的首项 ,
, ,
, ,
,
(1)求证:数列 为等比数列;
为等比数列;
(2)若 ,求最大的正整数
,求最大的正整数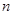 .
.
(1)证明见解析(2)99.
解析试题分析:(1)本小题关键是把递推关系式 配凑成
配凑成 与
与 的关系,再利用等比数列的定义加以说明即可;(2)本小题利用(1)的结论,可写出数列
的关系,再利用等比数列的定义加以说明即可;(2)本小题利用(1)的结论,可写出数列 的通项公式,由此可求出其前n项和,再利用已知条件的不等式可找到最大的正整数
的通项公式,由此可求出其前n项和,再利用已知条件的不等式可找到最大的正整数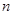 .
.
试题解析:(1)∵ ,∴
,∴ ,且
,且 ,∴数列
,∴数列 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
(2)由(1)可求得 ,∴
,∴ ,又
,又
 ,若
,若 ,则
,则 .
.
考点:由特殊递推关系构造新数列(等差或等比数列),定义法证明等比数列,等比数列通项公式,前n项和公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的通项公式
的通项公式 ,记
,记 ,试通过计算
,试通过计算 、
、 、
、 的值,推测出
的值,推测出 .
. ,过点P(-2,-4)的直线
,过点P(-2,-4)的直线  的参数方程为:
的参数方程为: (t为参数),直线
(t为参数),直线 成等比数列,求a的值
成等比数列,求a的值 的首项
的首项 .
. 是等比数列,并求出
是等比数列,并求出 ;
; .
. =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列. 的首项
的首项 ,且
,且
 .
. 的前
的前 项和
项和 .
. 中,已知
中,已知 ,
, ,
, .
.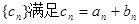 ,求
,求 的前
的前 项和
项和 .
. 中,
中, ,
, ,记
,记 为
为 项的和,
项的和, ,
, .
. 是否为等比数列,并求出
是否为等比数列,并求出 ;
;