题目内容
 如图(1),四边形ABCD为等腰梯形,AB∥CD,E,F分别为AB、CD的中点,且AB=4,CD=2,EF=1,现将四边形BCEF沿EF折起到四边形B1C1FE的位置,如图(2),使平面B1C1FE⊥平面AEFD.
如图(1),四边形ABCD为等腰梯形,AB∥CD,E,F分别为AB、CD的中点,且AB=4,CD=2,EF=1,现将四边形BCEF沿EF折起到四边形B1C1FE的位置,如图(2),使平面B1C1FE⊥平面AEFD.(1)求证:C1F∥平面AEB1;
(2)求证:AD⊥平面B1ED;
(3)线段B1D上是否存在一点G,使EG⊥平面AB1D,若存在求
| B1G |
| GD |
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:(1)由C1F∥B1E,证明C1F∥平面AEB1;
(2)由AD⊥DE,B1E⊥AD,且B1E∩DE=E,证明AD⊥平面B1ED;
(3)假设线段B1D上存在一点G,使EG⊥平面AB1D,得出EG⊥B1D即可,画出Rt△B1ED,EG⊥B1D,求出B1G与GD的值即可.
(2)由AD⊥DE,B1E⊥AD,且B1E∩DE=E,证明AD⊥平面B1ED;
(3)假设线段B1D上存在一点G,使EG⊥平面AB1D,得出EG⊥B1D即可,画出Rt△B1ED,EG⊥B1D,求出B1G与GD的值即可.
解答:
解:(1)证明:∵C1F∥B1E,
C1F?平面AEB1,
B1E?平面AEB1,
∴C1F∥平面AEB1;
(2)∵AE=
AB=2,DE=
=
=
,AD=
=2;
∴AB2=DE2+AD2,
∴AD⊥DE;
∵B1E⊥EF,平面B1C1FE⊥平面AEFD,
B1E?平面B1C1FE,平面B1C1FE∩平面AEFD=EF,
∴B1E⊥平面AEFD,
AD?平面AEFD,
∴B1E⊥AD;
又B1E∩DE=E,
B1E?平面B1ED,ED?平面B1ED,
∴AD⊥平面B1ED;
(3)设线段B1D上存在一点G,使EG⊥平面AB1D,
∵AD⊥平面B1ED,
EG?平面B1ED,
∴AD⊥EG;
只需过E点作EG⊥B1D,垂足为G,
∴EG⊥平面AB1D;
在Rt△B1ED中,EG⊥B1D,如图所示;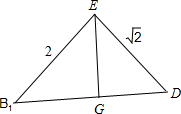
∴B1D=
=
,
∴EG=
=
=
,
∴B1G=
=
,
GD=
=
;
∴
=2;
即线段B1D上存在一点G,使EG⊥平面AB1D,且
=2.
C1F?平面AEB1,
B1E?平面AEB1,
∴C1F∥平面AEB1;
(2)∵AE=
| 1 |
| 2 |
| EF2+FD2 |
12+(
|
| 2 |
| 12+12 |
∴AB2=DE2+AD2,
∴AD⊥DE;
∵B1E⊥EF,平面B1C1FE⊥平面AEFD,
B1E?平面B1C1FE,平面B1C1FE∩平面AEFD=EF,
∴B1E⊥平面AEFD,
AD?平面AEFD,
∴B1E⊥AD;
又B1E∩DE=E,
B1E?平面B1ED,ED?平面B1ED,
∴AD⊥平面B1ED;
(3)设线段B1D上存在一点G,使EG⊥平面AB1D,
∵AD⊥平面B1ED,
EG?平面B1ED,
∴AD⊥EG;
只需过E点作EG⊥B1D,垂足为G,
∴EG⊥平面AB1D;
在Rt△B1ED中,EG⊥B1D,如图所示;

∴B1D=
| B1E2+ED2 |
| 6 |
∴EG=
| B1E•ED |
| BD |
2×
| ||
|
| 2 | ||
|
∴B1G=
| B1E2-ED2 |
|
GD=
| ED2-EG2 |
|
∴
| B1G |
| GD |
即线段B1D上存在一点G,使EG⊥平面AB1D,且
| B1G |
| GD |
点评:本题考查了空间中的平行与垂直的应用问题,也考查了空间想象能力与逻辑推理能力,是综合性题目.

练习册系列答案
相关题目
某校为了了解学生参加社会实践活动的意向,采用分层抽样从高一、高二、高三学生中抽取容量为200的样本进行调查,已知高一、高二、高三的学生人数之比为4:3:3,则应从高三学生中抽取的人数是( )
| A、30 | B、40 | C、60 | D、80 |
设R表示实数集,A=[-1,2],B=(0,+∞),则A∩∁RB等于( )
| A、(0,2] |
| B、(-∞,2] |
| C、(-1,+∞) |
| D、[-1,0] |
 如图所示的几何体中,四边形ABCD与BDEF是边长均为a的菱形,FA=FC
如图所示的几何体中,四边形ABCD与BDEF是边长均为a的菱形,FA=FC