题目内容
5.在一个盒子里装有6枝圆珠笔,其中3枝一等品,2枝二等品和一枝三等品,从中任取3枝,则恰有2枝一等品的概率是$\frac{9}{20}$.分析 恰有两枝一等品,从3支一等品中任取两支,从二、三等品种任取一支,利用分步乘法原理计算后除以基本事件总数.
解答 解:恰有两枝一等品的概率P=$\frac{{{C}_{3}^{2}C}_{3}^{1}}{{C}_{6}^{3}}$=$\frac{9}{20}$,
故答案为:$\frac{9}{20}$.
点评 本题考查了古典概型及其概率计算公式,考查了简单的组合问题,是基础的运算题.

练习册系列答案
相关题目
16.下列对于平面α、β、γ和直线a、b、l的说法错误的是( )
| A. | 若a∥α,b∥α,则a不一定平行于b | |
| B. | 若α不垂直于β,则α内一定不存在直线垂直于β | |
| C. | 若α⊥γ,β⊥γ,且α∩β=l,则l⊥γ | |
| D. | 若α⊥β,则α内一定不存在直线平行于β |
20.下列语句中的赋值语句是( )
| A. | x=x^3 | B. | 2=x | C. | x=y=2 | D. | x+y=z |
17.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x^2}+{y^2}≤4\\ x-y≥0\end{array}$,则z=$\sqrt{{{(x+4)}^2}+{{(y-4)}^2}}$的最大值和最小值分别为( )
| A. | $36+16\sqrt{2}$,32 | B. | $4\sqrt{2}+2$,$4\sqrt{2}$ | C. | $36+16\sqrt{2}$,$4\sqrt{2}$ | D. | $36+16\sqrt{2}$,36 |
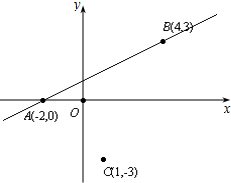 直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).
直角坐标系xOy中,点A坐标为(-2,0),点B坐标为(4,3),点C坐标为(1,-3),且$\overrightarrow{AM}$=t$\overrightarrow{AB}$(t∈R).