题目内容
已知y=f(x)是奇函数,当x∈(0,2)时,f(x)=lnx-ax ,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
,当x∈(-2,0)时,f(x)的最小值为1,则a的值等于( )
A.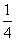 B.
B.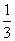
C.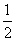 D.1
D.1
D解析 由题意知,当x∈(0,2)时,f(x)的最大值为-1.
令f′(x)= -a=0,得x=
-a=0,得x= ,
,
当0<x< 时,f′(x)>0;
时,f′(x)>0;
当x> 时,f′(x)<0.
时,f′(x)<0.
∴f(x)max=f =-lna-1=-1,解得a=1.
=-lna-1=-1,解得a=1.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
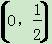 B.
B.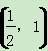
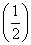 ,c=f(3),则( )
,c=f(3),则( )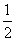 x2-cosx,x∈[-1,1],则导函数f′(x)是( )
x2-cosx,x∈[-1,1],则导函数f′(x)是( )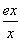 ,f(2)=
,f(2)=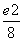 ,则x>0时,f(x)( )
,则x>0时,f(x)( ) .
. <b对x∈
<b对x∈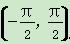 .
.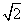 ,θ=
,θ=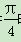 时,求f(x)在区间[0,π]上的最大值与最小值;
时,求f(x)在区间[0,π]上的最大值与最小值; =0,f(π)=1,求a,θ的值.
=0,f(π)=1,求a,θ的值.