题目内容
11．一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，表为抽样试验的结果：| 转速x（转/秒） | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y（件） | 11 | 9 | 8 | 5 |
分析 求出平均数$\overline{x}$、$\overline{y}$，代入公式计算回归方程的系数$\widehat{b}$与$\widehat{a}$，即可求出回归直线方程．
解答 解：x的平均数为$\overline{x}$=$\frac{1}{4}$（16+14+12+8）=12.5，
y的平均数为$\overline{y}$=$\frac{1}{4}$（11+9+8+5）=8.25，
且$\underset{\stackrel{4}{∑}}{i=1}$（xi-$\overline{x}$）（yi-$\overline{y}$）=25.5，$\underset{\stackrel{4}{∑}}{i=1}$${{（x}_{i}-\overline{x}）}^{2}$=35，
∴$\widehat{b}$=$\frac{25.5}{35}$≈0.7286，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=-0.8571；
∴回归直线方程为y=0.7286x-0.8571；
点评 本题考查了求线性回归方程的应用问题，也考查了计算能力的应用问题，是基础题目．
练习册系列答案
相关题目
1．下列关系中，表述正确的是（ ）
| A． | {0}∈{x|x2=x} | B． | {0}⊆{x|x2=x} | C． | 0∉{x|x2=x} | D． | 0⊆{x|x2=x} |
2．已知集合P={x|-4≤x≤4}，Q={y|-2≤y≤2}，则下列对应不能表示为从P到Q的函数的是（ ）
| A． | y=$\frac{1}{2}$x | B． | y2=$\frac{1}{2}$（x+4） | C． | y=$\frac{1}{4}$x2-2 | D． | y=-$\frac{1}{8}$x2 |
16．以下判断正确的是（ ）
| A． | x＞5是命题 | |
| B． | 命题“存在x∈R，x2+x-1＜0”的否定是“任意x∈R，x2+x-1＞0” | |
| C． | 命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为假命题 | |
| D． | “b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件 |
20．
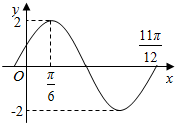已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象如图所示，若方程f（x）=m在区间[0，π]上有两个不同的数解x1、x2，则x1+x2的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象如图所示，若方程f（x）=m在区间[0，π]上有两个不同的数解x1、x2，则x1+x2的值为（ ）| A． | $\frac{π}{3}$ | B． | $\frac{2}{3}π$ | C． | $\frac{4}{3}π$ | D． | $\frac{π}{3}$或$\frac{4}{3}π$ |