题目内容
19.已知函数f(x)在(-1,1)上有定义,且f($\frac{1}{5}$)=$\frac{1}{2}$.对任意x,y∈(-1,1)都有f(x)+f(y)=f($\frac{x+y}{1+xy}$),当且仅当─1<x<0时,f(x)<0.(1)判断f(x)在(0,1)上的单调性,并说明理由;
(2)试求f($\frac{1}{2}$)-f($\frac{1}{11}$)-f($\frac{1}{19}$)的值.
(3)若将函数f(x)的定义域扩充为R单调性保持不变且关于x的不等式 f(x2-9)+f(kx+3k)>0在x∈(0,1)上恒成立,求实数k的取值范围.
分析 (1)根据函数单调性的定义即可判断f(x)在(0,1)上的单调性;
(2)根据函数奇偶性以及抽象函数之间的关系即可得到结论;
(3)化为具体不等式,再分离参数,即可求实数k的取值范围.
解答 解:(1)任取x1,x2∈(0,1),且0<x1<x2<1.
f(x2)-f(x1)=f(x2)+f(-x1)=f($\frac{{x}_{2}-{x}_{1}}{1-{x}_{1}{x}_{2}}$)=-f($\frac{{x}_{1}-{x}_{2}}{1-{x}_{1}{x}_{2}}$)
∵0<x1<x2<1,
∴(1-x1x2)-(x2-x1)=(1+x1)(1-x2)>0⇒1-x1x2>x2-x1>0⇒0<$\frac{{x}_{2}-{x}_{1}}{1-{x}_{1}{x}_{2}}$<1,
∴-1<$\frac{{x}_{1}-{x}_{2}}{1-{x}_{1}{x}_{2}}$<0,
∴f($\frac{{x}_{1}-{x}_{2}}{1-{x}_{1}{x}_{2}}$)>0,
∴-f($\frac{{x}_{1}-{x}_{2}}{1-{x}_{1}{x}_{2}}$)<0,
即f(x2)<f(x1).
故f(x)是(0,1)上的减函数.
(2)f($\frac{1}{2}$)-f($\frac{1}{11}$)=f($\frac{1}{2}$)+f(-$\frac{1}{11}$)=f($\frac{\frac{1}{2}-\frac{1}{11}}{1-\frac{1}{2}×\frac{1}{11}}$)=f($\frac{3}{7}$),
∴f($\frac{3}{7}$)-f($\frac{1}{19}$)=f($\frac{\frac{3}{7}-\frac{1}{19}}{1-\frac{3}{7}×\frac{1}{19}}$)=f($\frac{5}{13}$).
而f($\frac{1}{5}$)+f($\frac{1}{5}$)=f($\frac{5}{13}$)⇒f($\frac{5}{13}$)=2×f($\frac{1}{5}$)=1,
∴f($\frac{1}{2}$)-f($\frac{1}{11}$)-f($\frac{1}{19}$)=1;
(3)取x=y=0⇒f(0)=0,f(-x)+f(x)=f(0)=0⇒f(-x)=-f (x),又定义域对称,
故f(x)是(-1,1)上的奇函数
∵f(x2-9)+f(kx+3k)>0在R上是奇函数
∴f(x2-9)>-f(kx+3k)=f(-kx-3k)在 x∈(0,1)上恒成立
由(1)知函数f(x)在R上单调递增
∴x2-9>-kx-3k,
即x2+kx+3k-9>0在 x∈(0,1)上恒成立.
∴(x+3)k>9-x2
∵x∈(0,1),∴3-x>0
∴k>3-x在 x∈(0,1)上恒成立.
令h(x)=3-x,x∈(0,1),则2<h(x)<3
∴k≥3.
故k的取值范围为{k|k≥3}.
点评 本题主要考查抽象函数的应用,根据函数奇偶性和单调性的定义是解决本题的关键.综合考查函数的性质的应用.

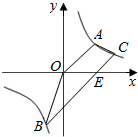 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.(1)求反比例函数的解析式;
(2)求四边形AOEC的面积.
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
 ,
, 的整数部分用
的整数部分用 表示,则
表示,则 的值为( )
的值为( )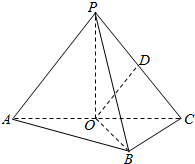 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.