题目内容
6.(1)化简$\root{3}{{a}^{\frac{9}{2}}\sqrt{{a}^{-3}}}$÷$\sqrt{\root{3}{{a}^{-7}}}$•$\root{3}{{a}^{13}}$;(2)解不等式ax+5<a4x-1(a>0,且a≠1)
分析 (1)化根式为分数指数幂,然后利用有理指数幂的运算性质求得答案;
(2)对a分类,然后利用指数式的单调性化指数不等式为一次不等式求解.
解答 解:(1)$\root{3}{{a}^{\frac{9}{2}}\sqrt{{a}^{-3}}}$÷$\sqrt{\root{3}{{a}^{-7}}•\root{3}{{a}^{13}}}$
=$({a}^{\frac{9}{2}}•{a}^{-\frac{3}{2}})^{\frac{1}{3}}$$÷({a}^{-\frac{7}{3}}•{a}^{\frac{13}{3}})^{\frac{1}{2}}$
=1;
(2)当a>1时,原不等式可变为x+5<4x-1,解得x>2;
当0<a<1时,原不等式可变为x+5>4x-1,解得x<2.
故当a>1时,原不等式的解集为(2,+∞);
当0<a<1时,原不等式的解集为(-∞,2).
点评 本题考查有理指数幂的化简与求值,考查了指数不等式的解法,是基础题.

练习册系列答案
相关题目
11.一台机器使用的时间较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,表为抽样试验的结果:
假设y对x有线性相关关系,求回归直线方程;$\widehat{b}$=$\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)÷\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y(件) | 11 | 9 | 8 | 5 |
16.已知函数f(x)=3x-3|x|,若3tf(2t)-mf(t)≥0对于t∈[-2,-1]恒成立,则实数m范围是( )
| A. | [$\frac{1}{9}$,+∞) | B. | (-∞,$\frac{1}{9}$] | C. | [$\frac{10}{9}$,+∞) | D. | (-∞,$\frac{10}{9}$] |
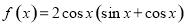 的最大值和最小正周期分别是 ( )
的最大值和最小正周期分别是 ( )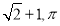 C. 2,2π D.
C. 2,2π D.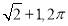
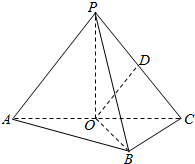 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.