题目内容
在△ABC中,设A、B、C的对边分别为a、b、c,向量 ,
, ,若
,若
(1)求角A的大小;
(2)若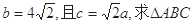 的面积.
的面积.
(1) ;(2)16.
;(2)16.
解析试题分析:
解题思路:(1)利用平面向量的模长公式将条件转化为 ,再结合角的范围求角A;(2)由正弦定理将边的关系化成角的正弦的关系,进而判定三角形的形状和求三角形的面积.
,再结合角的范围求角A;(2)由正弦定理将边的关系化成角的正弦的关系,进而判定三角形的形状和求三角形的面积.
规律总结:以平面向量为载体考查三角函数问题,体现了平面向量的工具性,要灵活选择平面向量知识合理化简,出现三角函数关系式;根据三角函数值求角的,要注意结合所给角的范围;解三角形要根据条件合理选择正弦定理、余弦定理、面积公式.
试题解析:
(1)



又 ,
,

 ,
,
 ,
,
 为等腰三角形,
为等腰三角形, .
.
考点:1.平面向量的模长;2.解三角形.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知 ABC外接圆O的半径为1,且
ABC外接圆O的半径为1,且  ,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为
,从圆O内随机取一个点M,若点M取自△ABC内的概率恰为 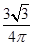 ,则
,则 MBC的形状为
MBC的形状为
| A.直角三角形 | B.等边三角形 | C.钝角三角形 | D.等腰直角三角形 |
 .已知
.已知
 ,求△ABC外接圆半径.
,求△ABC外接圆半径. 中,角
中,角 对的边分别为
对的边分别为 ,且
,且 .
. 的值;
的值; ,求
,求 .
. 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知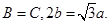
 的值;(2)
的值;(2) 的值.
的值. 的三个内角
的三个内角 成等差数列,它们的对边分别为
成等差数列,它们的对边分别为 ,且满足
,且满足 ,
, .
. ;
; .
. 中,
中, ,
, ,
, .
. 长;
长; 的值.
的值.
 (x≥0),
(x≥0), ,求用
,求用 表示
表示 的函数关系式,并求函数的定义域;
的函数关系式,并求函数的定义域; 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, 中,已知
中,已知 ,
, ,
, ,则
,则