题目内容
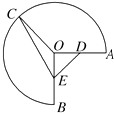
【题目】直线y=kx﹣1与曲线 
有两个不同的公共点，则k的取值范围是 ．
【答案】（0,
]
【解析】解：根据题意得：y=kx﹣1为恒过定点（0，﹣1）的直线，
曲线表示圆心为（2，0），半径为1的下半圆，如图所示，
当直线与圆D相切时，有 
=1，
解得：k=0或k= 
（不合题意，舍去）；
把C（3，0）代入y=kx﹣1，得k= 
，
∴k的取值范围是（0， ]．
所以答案是：（0， ]．
【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点，需要掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．
练习册系列答案
相关题目
