题目内容
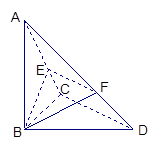
如图1,在平面内,ABCD 是
是 且
且 的菱形,
的菱形, 和
和 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使 与
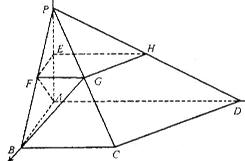
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。

(1)设二面角E – AC – D1的大小为q,若 ,求
,求 的取值范围;
的取值范围;
(2)在线段 上是否存在点
上是否存在点 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
解:设菱形 的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系如图3。设BE =" t" (t > 0)
的中心为O,以O为原点,对角线AC,BD所在直线分别为x,y轴,建立空间直角坐标系如图3。设BE =" t" (t > 0)
(1)

设平面 的法向量为
的法向量为 ,则
,则 ,令
,令 得
得 。
。 设平面
设平面 的法向量为
的法向量为 ,则
,则 ,令
,令
 得
得 。
。
设二面角 的大小为
的大小为 ,则
,则 。
。
∵
 ∴
∴

 ,
,
解得 £ t £
£ t £ 。
。
解析

练习册系列答案
相关题目

 更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是
更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是 高度增加4M(底面直径不变)。
高度增加4M(底面直径不变)。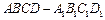 中,E、F、G分别为
中,E、F、G分别为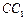 、
、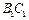 、
、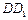 的中点,O为
的中点,O为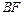 与
与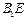 的交点,
的交点,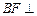 面
面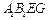
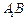 与平面
与平面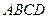 的边长为1,分别取边
的边长为1,分别取边 的中点
的中点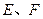 ,连结
,连结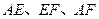 ,
,  重合于一点
重合于一点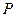 ,得到一
,得到一 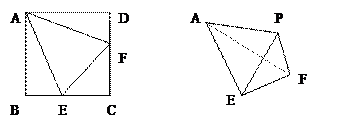
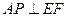 ;
;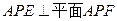 。
。 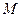 、
、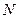 分别是
分别是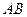 、
、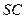 的中点,
的中点,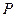 是
是 上的一动点。
上的一动点。
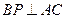 ;
;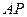 平行于平面
平行于平面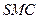 ?
?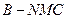 的体积。
的体积。
 为
为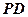 的中点,求证
的中点,求证 :
: 平面
平面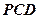 ;
; 与平面
与平面