题目内容
已知数列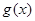 的前n项和为
的前n项和为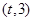 ,
,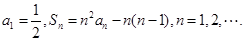
(1)证明:数列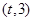 是等差数列,并求
是等差数列,并求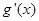 ;
;
(2)设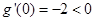 ,求证:
,求证: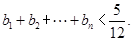
 的前n项和为
的前n项和为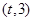 ,
,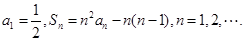
(1)证明:数列
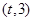 是等差数列,并求
是等差数列,并求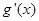 ;
;(2)设
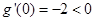 ,求证:
,求证: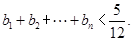
(1)证明略, ,(2)详见解析.
,(2)详见解析.
 ,(2)详见解析.
,(2)详见解析.试题分析:(1)利用
 代入
代入 得关于
得关于 的递推公式,然后变形为
的递推公式,然后变形为 ,利用等差数列的定义即可说明;
,利用等差数列的定义即可说明;(2)由已知可得
 ,利用裂项求和法求
,利用裂项求和法求 ,然后放缩一下即可.
,然后放缩一下即可.试题解析:(1)证明:由
 知,当
知,当 时:
时: ,
,即
 ,∴
,∴ ,对
,对 成立.
成立.又
 是首项为1,公差为1的等差数列.
是首项为1,公差为1的等差数列. ,∴
,∴ .6分
.6分(2)
 ,8分
,8分∴

=
 .12分
.12分
练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
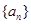 中,已知
中,已知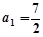 ,
,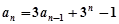 (
(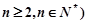 .
.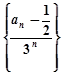 是等差数列;
是等差数列;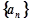 的通项公式
的通项公式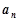 及它的前
及它的前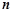 项和
项和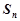 .
.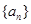 的各项均为正数,其前
的各项均为正数,其前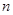 项和为
项和为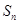 ,且
,且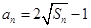 ,
,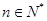 ,数列
,数列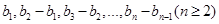 是首项和公比均为
是首项和公比均为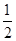 的等比数列.
的等比数列.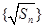 是等差数列;
是等差数列;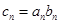 ,求数列
,求数列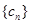 的前
的前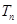 .
.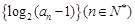 为等差数列,且
为等差数列,且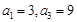 .
.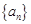 的通项公式;
的通项公式;
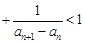 .
.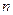 项和为Sn.已知S3=
项和为Sn.已知S3=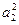 ,且S1,S2,S4成等比数列,则{an}的通项式为( )
,且S1,S2,S4成等比数列,则{an}的通项式为( )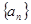 ,规定
,规定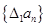 为数列
为数列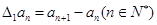 .
.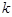 ,规定
,规定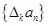 为
为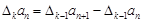 .若数列
.若数列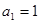 ,
,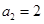 ,且满足
,且满足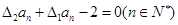 ,则
,则 .
. 中,若
中,若 ,则
,则 等于
等于 中,已知
中,已知 ,则
,则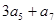 = ( )
= ( )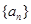 的前
的前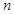 项和为
项和为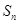 ,若
,若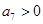 ,
,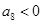 ,则下列结论正确的是( )
,则下列结论正确的是( )


