题目内容
已知直线l的参数方程:
(t为参数)与圆C的极坐标方程:ρ=2
sin(θ+
),则直线l与C的公共点个数是 .
|
| 2 |
| π |
| 4 |
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:分别把直线的参数方程化为普通方程,极坐标方程化为直角坐标方程,再利用点到直线的距离公式得出圆心到直线的距离d,与半径r比较即可得出.
解答:
解:直线l的参数方程:
(t为参数),化为y=1+2x,即2x-y+1=0.
圆C的极坐标方程:ρ=2
sin(θ+
),展开ρ=2
×
(sinθ+cosθ),化为ρ2=2ρsinθ+2ρcosθ,
∴x2+y2=2x+2y,化为(x-1)2+(y-1)2=2.
圆心C(1,1)到直线l的距离d=
=
<
=r,
∴直线与圆相交,有两个公共点.
故答案为:2.
|
圆C的极坐标方程:ρ=2
| 2 |
| π |
| 4 |
| 2 |
| ||
| 2 |
∴x2+y2=2x+2y,化为(x-1)2+(y-1)2=2.
圆心C(1,1)到直线l的距离d=
| |2-1+1| | ||
|
| 2 | ||
|
| 2 |
∴直线与圆相交,有两个公共点.
故答案为:2.
点评:本题考查了把直线的参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式、直线与圆的位置关系判定,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
如图是计算
+
+
+
+
值的一个程序框图,其中判断框内应填入的条件是( )
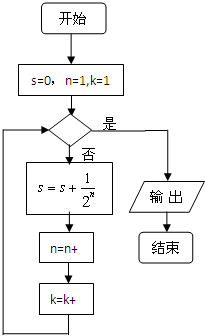
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 16 |
| 1 |
| 32 |

| A、K>5? | B、K<5? |
| C、K>10? | D、K<10? |
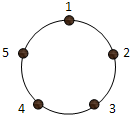 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按瞬时针方向绕圆从一个点跳到下一个点.若它停在奇数点上,则下一次只能跳一个点,若停在偶数点上,则可以连续跳2个点.该青蛙从5这点起跳,经2009次跳后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
已知
=(-2,0),
=(0,2)(O为坐标原点),点C在曲线
(θ为参数)上运动,则△ABC面积的最大值为( )
| OA |
| OB |
|
A、3-
| ||||
B、3+
| ||||
C、
| ||||
D、
|
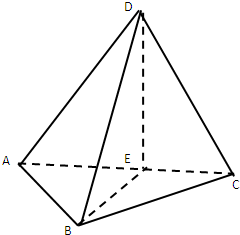 如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.
如图,三棱锥D-ABC中,AB=BC=2,BD=3,∠ABC=∠DBA=∠DBC=60°,E为AC的中点.