Question

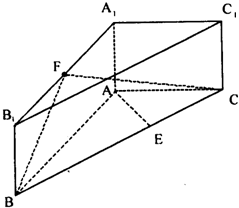（2006•东城区三模）如图，已知直三棱柱ABC-A₁B₁C₁，∠CAB=90°，AB=2，AA₁=1，AC=

2 3

3

，AE⊥BC于E，F为A₁B₁的中点．
（1）求异面直线AE与BF所成角的大小；
（2）求二面角A-BF-C的大小；
（3）求点A到平面BCF的距离．

Answer 1

分析：（1）在直三棱柱ABC-A₁B₁C₁中，以AB所在的直线为x轴，以AC所在的直线为y轴，AA₁所在的直线为z轴建立如图所示空间直角坐标系，求出

AE

与

BF

的坐标，直接由两向量所成的角求解异面直线AE与BF所成角的大小；
（2）求出二面角A-BF-C的两个半平面所在平面的法向量，利用平面法向量所成的角求解二面角的大小；
（3）利用空间向量求点A到平面BCF的距离．

解答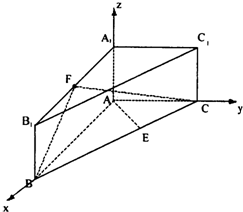：解：（1）在直三棱柱ABC-A₁B₁C₁中，
以AB所在的直线为x轴，以AC所在的直线为y轴，AA₁所在的直线为z轴建立如图所示空间直角坐标系．
由已知AB=2，AA₁=1，AC=

2

3

3

．
可得A（0，0，0），B（2，0，0），E（

1

2

，

3

2

，0），F（1，0，1），C（0，

2 3

3

，0）．

AE

=(

1

2

，

3

2

，0)，

BC

=(-2，

2 3

3

，0)，

BF

=(-1，0，1)
∴cos＜

AE

，

BF

＞=

AE • BF

| AE || BF |

=

- 1 2

2

=-

2

4

∴异面直线AE与BF所成角的大小为arccos

2

4

；
（2）设

n

=(x，y，z)是平面BCF的一个法向量，
由

n • BF =0 n • BC =0.

可得

-x+z=0 2x- 2 3 3 y=0.

即

x=z 3 x=y.

令z=1，可得

n

=(1，

3

，1)．
取平面ABF的一个法向量为

m

=(0，1，0)
cos＜

n

，

m

＞=

n • m

| n || m |

=

3

5

=

15

5

即二面角A-BF-C的大小为arccos

15

5

．
（3）点A到平面BCF的距离，即

AB

在平面BCF的法向量

n

的投影的绝对值，
所以距离d=||

AB

|cos＜

AB

，

n

＞|=

| AB • n |

| n |

=

2 5

5

．
所以点A到平面BCF的距离为

2 5

5

．

点评：本题考查了利用空间向量求空间角的问题，解答的关键是建立正确的空间右手系，同时注意利用空间向量求空间叫何空间距离的公式，是中档题．