题目内容
已知 =(2cosx+2
=(2cosx+2 sinx,1),
sinx,1), =(cosx,-y),且
=(cosx,-y),且 ⊥
⊥ .
.
(1)将y表示为x的函数f(x),并求f(x)的单调增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f( )=3,且a=2,b+c=4,求△ABC的面积.
)=3,且a=2,b+c=4,求△ABC的面积.
解:(1)由题意可得(2cosx+2 sinx)cosx-y=0,
sinx)cosx-y=0,
即y=f(x)=(2cosx+2 sinx)cosx=2cos2x+2
sinx)cosx=2cos2x+2 sinxcosx
sinxcosx
=1+cos2x+ sin2x=1+2sin(2x+
sin2x=1+2sin(2x+ ),
),
由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,得kπ-
,得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,
故f(x)的单调增区间为[kπ- ,kπ+
,kπ+ ],k∈Z
],k∈Z
(2)由(1)可知f(x)=1+2sin(2x+ ),
),
故f( )=1+2sin(A+
)=1+2sin(A+ )=3,解得sin(A+
)=3,解得sin(A+ )=1
)=1
故可得A+ =
= ,解得A=
,解得A= ,
,
由余弦定理可得22=b2+c2-2bccosA,
化简可得4=b2+c2-bc=(b+c)2-3bc=16-3bc,
解得bc=4,故△ABC的面积S=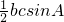 =
=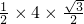 =
=
分析:(1)由数量积为0可得方程,由三角函数的公式化简可得f(x),再由2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,可得单调递增区间;
,可得单调递增区间;
(2)结合(1)可得f( )=1+2sin(A+
)=1+2sin(A+ )=3,进而可得A=
)=3,进而可得A= ,由余弦定理可得bc=4,代入面积公式S=
,由余弦定理可得bc=4,代入面积公式S=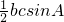 ,计算可得答案.
,计算可得答案.
点评:本题考查三角函数的性质和余弦定理的应用,涉及向量的垂直的判断,属基础题.
 sinx)cosx-y=0,
sinx)cosx-y=0,即y=f(x)=(2cosx+2
 sinx)cosx=2cos2x+2
sinx)cosx=2cos2x+2 sinxcosx
sinxcosx=1+cos2x+
 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+ ),
),由2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,得kπ-
,得kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,
,k∈Z,故f(x)的单调增区间为[kπ-
 ,kπ+
,kπ+ ],k∈Z
],k∈Z(2)由(1)可知f(x)=1+2sin(2x+
 ),
),故f(
 )=1+2sin(A+
)=1+2sin(A+ )=3,解得sin(A+
)=3,解得sin(A+ )=1
)=1故可得A+
 =
= ,解得A=
,解得A= ,
,由余弦定理可得22=b2+c2-2bccosA,
化简可得4=b2+c2-bc=(b+c)2-3bc=16-3bc,
解得bc=4,故△ABC的面积S=
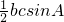 =
=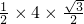 =
=
分析:(1)由数量积为0可得方程,由三角函数的公式化简可得f(x),再由2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,可得单调递增区间;
,可得单调递增区间;(2)结合(1)可得f(
 )=1+2sin(A+
)=1+2sin(A+ )=3,进而可得A=
)=3,进而可得A= ,由余弦定理可得bc=4,代入面积公式S=
,由余弦定理可得bc=4,代入面积公式S=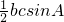 ,计算可得答案.
,计算可得答案.点评:本题考查三角函数的性质和余弦定理的应用,涉及向量的垂直的判断,属基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目