Question

已知函数在处取得极值．

（I）求与满足的关系式；

（II）若，求函数的单调区间；

（III）若，函数，若存在，，使得

成立，求的取值范围．

 

Answer 1

【答案】

（Ⅰ）．   （Ⅱ）单调递增区间为，，单调递减区间为． （Ⅲ）的取值范围是． 

【解析】本题考查导数知识的运用，考查函数的单调性，考查恒成立问题，解题的关键是正确求导，确定分类标准，利用函数的最值解决恒成立问题。

（Ⅰ）求导函数，利用函数在x=1处取得极值，可得a与b满足的关系式；

（Ⅱ）确定函数f（x）的定义域，求导函数，确定分类标准，从而可得函数f（x）的单调区间；

（Ⅲ）当a＞3时，确定f（x）在上的最大值，g（x）在上的最小值，要使存在m₁，m₂∈[

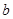使得|f（m₁）-g（m₂）|＜9成立，只需要|f（x）_max-g（x）_min|＜9，即可求得a的取值范围．