题目内容
设函数f(x)是实数集R上的增函数,令F(x)=f(x)-f(2-x).
(1)求证:F(x)在R是增函数;
(2)若F(x1)+F(x2)>0,求证:x1+x2>2.
答案:
解析:
解析:
证明:(1)任取x1、x2∈R,且x1<x2,
∵f(x)在R上是增函数,
∴f(x1)<f(x2),f(2-x1)>f(2-x2),
即f(x1)-f(x2)<0,f(2-x1)-f(2-x2)>0.
∴F(x1)-F(x2)=[f(x1)-f(2-x1)]-[f(x2)-f(2-x2)]
=[f(x1)-f(x2)]+[f(2-x2)-f(2-x1)]<0,
即F(x1)<F(x2).
∴F(x)在R上是增函数.
(2)∵F(x1)+F(x2)>0,
∴F(x1)>-F(x2).
而-F(x2)=-[f(x2)-f(2-x2)]
=f(2-x2)-f(x2)
=f(2-x2)-f[2-(2-x2)]
=F(2-x2).
∴F(x1)>F(2-x2).
又∵F(x)在R上是增函数,
∴x1>2-x2,即x1+x2>2.
思路分析:无论给出的函数式子多么复杂,只要是证明单调性,主要用“定义法”,要是比较自变量的大小,一般用单调性定义的逆命题.这就是解题思路,在正确的思路指导下,必能攻无不克,战无不胜.

练习册系列答案
相关题目
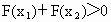 ,求证:
,求证: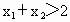 .
.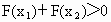 ,求证:
,求证: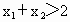 .
.