题目内容
14.△ABC的三个内角为A,B,C,若$\frac{\sqrt{3}cosA+sinA}{\sqrt{3}sinA-cosA}$=tan(-$\frac{7}{12}$π),则2cosB+sin2C的最大值为$\frac{3}{2}$.分析 根据书籍可得A=$\frac{π}{4}$,进而将2cosB+sin2C化为-2[cos($\frac{π}{4}$+C)+$\frac{1}{2}$]2+$\frac{3}{2}$,结合二次函数的图象和性质,可得答案.
解答 解:∵$\frac{\sqrt{3}cosA+sinA}{\sqrt{3}sinA-cosA}$=$-\frac{2sin(A+\frac{π}{3})}{2cos(A+\frac{π}{3})}$=$-tan(A+\frac{π}{3})$=tan(-$\frac{7}{12}$π)=-tan($\frac{7}{12}$π),
∴$tan(A+\frac{π}{3})$=tan($\frac{7}{12}$π),
∴$A+\frac{π}{3}$=$\frac{7}{12}$π+kπ,k∈Z,
又由A为三角形内角,
∴A=$\frac{π}{4}$,
∴2cosB+sin2C=-2cos(A+C)+sin2C=-2cos($\frac{π}{4}$+C)-cos($\frac{π}{2}$+2C)=-2cos2($\frac{π}{4}$+C)-2cos($\frac{π}{4}$+C)+1=-2[cos($\frac{π}{4}$+C)+$\frac{1}{2}$]2+$\frac{3}{2}$≤$\frac{3}{2}$,
故2cosB+sin2C的最大值为:$\frac{3}{2}$
故答案为:$\frac{3}{2}$
点评 本题考查的知识点是三角函数的恒等变换及应用,函数的最值,二次函数的图象和性质,难度中档.

练习册系列答案
相关题目
19.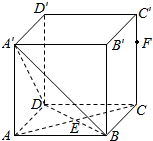 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
 如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )
如图,正方体ABCD-A′B′C′D′中,$\overrightarrow{BD}=2\overrightarrow{BE}$.设点F在线段CC'上,直线EF与平面A'BD所成的角为α,则sinα的取值范围是( )| A. | $[\frac{{\sqrt{3}}}{3},1]$ | B. | $[\frac{{2\sqrt{2}}}{3},1]$ | C. | $[\frac{{\sqrt{6}}}{3},\frac{{2\sqrt{2}}}{3}]$ | D. | $[\frac{{\sqrt{6}}}{3},1]$ |
3.设直线x-$\sqrt{3}$y+3=0与圆心为O的圆x2+y2=3交于A,B两点,则直线AO与BO的倾斜角之和为( )
| A. | $\frac{7π}{6}$ | B. | $\frac{5π}{4}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |