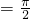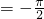题目内容
直线
，
都是函数f（x）=sin（ωx+ϕ）（ω＞0，-π＜ϕ≤π）的对称轴，且函数f（x）在区间
上单调递减，则（ ）A．ω=6，
B．ω=6，
C．ω=3，
D．ω=3，
【答案】分析：由题意求出函数的周期，利用周期公式求出ω，结合-π＜ϕ≤π，利用对称轴求出ϕ的值，即可得到选项．
解答：解：直线
，
都是函数f（x）=sin（ωx+ϕ）（ω＞0，-π＜ϕ≤π）的对称轴，且函数f（x）在区间
上单调递减，所以T=2×（
）=
；
所以ω=
=6，并且1=sin（6×
+ϕ），-π＜ϕ≤π，所以，ϕ=
；
故选A．
点评：本题是基础题，考查三角函数的图象的应用，函数的基本性质，考查计算能力，推理能力．
解答：解：直线
，都是函数f（x）=sin（ωx+ϕ）（ω＞0，-π＜ϕ≤π）的对称轴，且函数f（x）在区间上单调递减，所以T=2×（）=；所以ω=
=6，并且1=sin（6×+ϕ），-π＜ϕ≤π，所以，ϕ=；故选A．
点评：本题是基础题，考查三角函数的图象的应用，函数的基本性质，考查计算能力，推理能力．
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
直线x=
，x=
都是函数f（x）=sin（ωx+?）（ω＞0，-π＜?≤π）的对称轴，且函数f（x）在区间[
，
]上单调递减，则（ ）
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
A、ω=6，φ=
| ||
B、ω=6，φ=-
| ||
C、ω=3，φ=
| ||
D、ω=3，φ=-
|
，
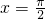都是函数f（x）=sin（ωx+?）（ω＞0，-π＜?≤π）的对称轴，且函数f（x）在区间
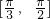上单调递减，则
