Question

15、已知函数f（x）的定义域为R，且对于任意x∈R，都有f（x）=f（-x）及f（x+4）=f（x）+f（2）成立．当x₁、x₂∈[0，2]且x₁≠x₂时，都有[f（x₁）-f（x₂）]（x₁-x₂）＞0成立．现给出下列四个结论：
①f（2）=0；②函数f（x）在区间[-6，-4]上为增函数；③直线x=-4是函数f（x）的一条对称轴；④方程f（x）=0在区间[-6，6]上有4个不同的实根．
其中正确命题的序号是

①③④

． （把你认为正确的命题序号都填上）

Answer 1

分析：由函数f（x）的定义域为R，且对于任意x∈R，都有f（x）=f（-x），易得函数f（x）为偶函数，又由当x₁、x₂∈[0，2]且x₁≠x₂时，都有[f（x₁）-f（x₂）]（x₁-x₂）＞0成立．则函数f（x）在区间[0，2]上为增函数，又由f（x+4）=f（x）+f（2），易得函数是T=4的周期函数，然后对四个结论逐一进行判断，即可得到答案．

解答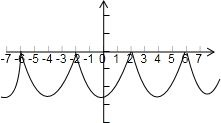：解：∵函数f（x）的定义域为R，
又∵对于任意x∈R，都有f（x）=f（-x），
∴函数f（x）为偶函数，
又∵当x₁、x₂∈[0，2]且x₁≠x₂时，
都有[f（x₁）-f（x₂）]（x₁-x₂）＞0成立．
∴函数f（x）在区间[0，2]上为增函数，
又∵f（x+4）=f（x）+f（2），
∴函数是T=4的周期函数，
则函数草图如下图所示：
由图易得：f（2）=0，故①正确；
函数f（x）在区间[-6，-4]上为减函数，故②错误；
直线x=-4是函数f（x）的一条对称轴，故③正确
方程f（x）=0在区间[-6，6]上有-6，-2，2，6共4个不同的实根．故④正确
故答案为：①③④

点评：当遇到函数综合应用时，处理的步骤一般为：①根据“让解析式有意义”的原则，先确定函数的定义域；②再化简解析式，求函数解析式的最简形式，并分析解析式与哪个基本函数比较相似；③根据定义域和解析式画出函数的图象④根据图象分析函数的性质．