题目内容
设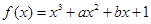 的导数
的导数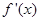 满足
满足 ,其中
,其中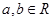 .
.
 求曲线
求曲线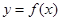 在点
在点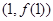 处的切线方程;
处的切线方程;
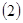 设
设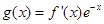 ,求函数
,求函数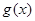 的极值.
的极值.
【答案】
(I)
(II)函数 处取得极小值
处取得极小值 处取得极大值
处取得极大值
【解析】
试题分析:(I)因 故
故
令 由已知
由已知
又令 由已知
由已知 因此
因此 解得
解得 因此
因此
又因为 故曲线
故曲线 处的切线方程为
处的切线方程为

(II)由(I)知 ,从而有
,从而有
令
当 上为减函数;
上为减函数;
当 在(0,3)上为增函数;
在(0,3)上为增函数;
当 时,
时, 上为减函数;
上为减函数;
从而函数 处取得极小值
处取得极小值 处取得极大值
处取得极大值
考点:导数的几何意义,利用导数研究函数的极值。
点评:典型题,在给定区间,导数非负,函数为增函数,导数非正,函数为减函数。求函数的极值问题,基本步骤是“求导数、求驻点、研究单调性、求极值”。

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
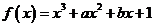 的导数
的导数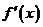 满足
满足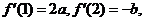 其中常数
其中常数 .
. 在点
在点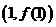 处的切线方程。
处的切线方程。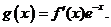 求函数
求函数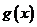 的极值。
的极值。