题目内容
某班级有52名学生，要从中抽取10名学生调查学习情况，若采用系统抽样方法，则此班内每个学生被抽到的机会是 ．
考点：古典概型及其概率计算公式,系统抽样方法
专题：概率与统计
分析：在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，在剔除过程中，每个个体被剔除的概率相等，每个个体被抽到包括两个过程，这两个过程是相互独立的；用每名学生不被剔除的概率乘以他被选中的概率，即可求出每个学生被抽到的机会是多少．
解答：
解：首先从52名学生中剔除2人，剩下的50名学生再按系统抽样的方法抽10名，
∵在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，
在剔除过程中，每个个体被剔除的概率相等，
∴每个个体被抽到包括两个过程，一是不被剔除，二是选中，这两个过程是相互独立的，
∴每人入选的概率P=
×
=
．
故答案为：
．
∵在系统抽样中，若所给的总体个数不能被样本容量整除，则要先剔除几个个体，然后再分组，
在剔除过程中，每个个体被剔除的概率相等，
∴每个个体被抽到包括两个过程，一是不被剔除，二是选中，这两个过程是相互独立的，
∴每人入选的概率P=
| 50 |
| 52 |
| 10 |
| 50 |
| 5 |
| 26 |
故答案为：
| 5 |
| 26 |
点评：本题主要考查了古典概型及其计算公式，系统抽样法的运用，属于基础题，解答此题的关键是要明确：当在系统抽样过程中比值不是整数时，需要用简单随机抽样的方法从总体中删除一些个体．
练习册系列答案
相关题目
如图，椭圆的中心在坐标原点O，顶点分别为A1，A2，B1，B2，焦点分别为F1，F2，延长B1F2与A2B2交于P点，若∠B1PB2为锐角，则此椭圆离心率e的取值范围是若函数f(x)=
(a，b，c，d∈R)的图象如图所示，则a：b：c：d=（ ）
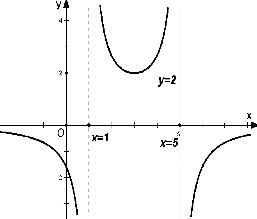
| d |
| ax2+bx+c |
| A、1：6：5：8 |
| B、1：6：5：（-8） |
| C、1：（-6）：5：8 |
| D、1：（-6）：5：（-8） |