题目内容
20.已知椭圆的中心在原点,焦点在x轴上,短轴长为10,离心率为$\frac{2}{3}$.(1)求椭圆的标准方程;
(2)求以椭圆焦点为顶点,顶点为焦点的双曲线的标准方程.
分析 (1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),运用离心率公式和a,b,c的关系,解方程可得a,b,进而得到椭圆方程;
(2)求得椭圆的焦点和左右顶点,可设双曲线的方程$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m,n>0),求得m,n,即可得到双曲线的方程.
解答 解:(1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意可得2b=10,e=$\frac{c}{a}$=$\frac{2}{3}$,a2-b2=c2,
解得b=5,a=3$\sqrt{5}$,c=2$\sqrt{5}$,
即有椭圆的方程为$\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1;
(2)设双曲线的方程为$\frac{{x}^{2}}{{m}^{2}}$-$\frac{{y}^{2}}{{n}^{2}}$=1(m,n>0),
由椭圆的焦点为(±2$\sqrt{5}$,0),可得m=2$\sqrt{5}$,
由椭圆的左右顶点为(±3$\sqrt{5}$,0),
可得$\sqrt{{m}^{2}+{n}^{2}}$=3$\sqrt{5}$,
解得n=5,
即有双曲线的方程为$\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1.
点评 本题考查椭圆和双曲线的方程的求法,注意运用椭圆的离心率公式和双曲线的性质,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.“b≠0”是“复数a+bi(a,b∈R)是纯虚数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
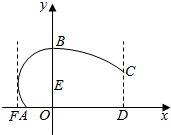 某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).
某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示:曲线AB是以点E为圆心的圆的一部分,其中E(0,t)(0<t≤25);曲线BC是抛物线y=-ax2+50(a>0)的一部分;CD⊥AD,且CD恰好等于圆E的半径.假定拟建体育馆的高OB=50(单位:米,下同).