题目内容
(本题满分12分)已知函数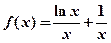 .
.
(Ⅰ)若函数在区间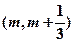 (其中
(其中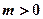 )上存在极值,求实数
)上存在极值,求实数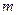 的取值范围;
的取值范围;
(Ⅱ)如果当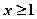 时,不等式
时,不等式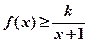 恒成立,求实数
恒成立,求实数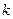 的取值范围;
的取值范围;
(Ⅲ)求证: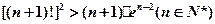 .
.
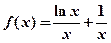 .
.(Ⅰ)若函数在区间
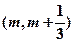 (其中
(其中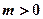 )上存在极值,求实数
)上存在极值,求实数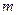 的取值范围;
的取值范围;(Ⅱ)如果当
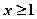 时,不等式
时,不等式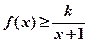 恒成立,求实数
恒成立,求实数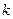 的取值范围;
的取值范围;(Ⅲ)求证:
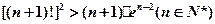 .
.(1) (2)
(2) (3)略
(3)略
 (2)
(2) (3)略
(3)略(Ⅰ)∵ ,则
,则 。
。
当 时,
时, ;当
;当 时,
时, 。
。
∴ 在
在 上单调递增,在
上单调递增,在 上单调递减 ∴
上单调递减 ∴ 在
在 取极大值
取极大值
∵ 在区间
在区间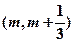 (其中
(其中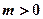 )上存在极值
)上存在极值
∴ ∴
∴ 即m的取值范围为
即m的取值范围为 。
。
(Ⅱ) ,记
,记
则
令 ,则
,则 ∵
∵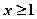 ∴
∴
∴ 在
在 上单调递增 ∴
上单调递增 ∴ 从而
从而
∴ 在
在 上也单调递增 ∴
上也单调递增 ∴
则k的取值范围为 。
。
(Ⅲ)由(Ⅱ)知 恒成立,即
恒成立,即 ,
,
令 ,则
,则 ,
,
∴ ,
, ,…,
,…,
叠加得: …
… …
…

∴ …
… ∴
∴ 。
。
 ,则
,则 。
。当
 时,
时, ;当
;当 时,
时, 。
。∴
 在
在 上单调递增,在
上单调递增,在 上单调递减 ∴
上单调递减 ∴ 在
在 取极大值
取极大值∵
 在区间
在区间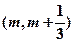 (其中
(其中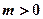 )上存在极值
)上存在极值∴
 ∴
∴ 即m的取值范围为
即m的取值范围为 。
。(Ⅱ)
 ,记
,记
则

令
 ,则
,则 ∵
∵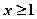 ∴
∴
∴
 在
在 上单调递增 ∴
上单调递增 ∴ 从而
从而
∴
 在
在 上也单调递增 ∴
上也单调递增 ∴
则k的取值范围为
 。
。(Ⅲ)由(Ⅱ)知
 恒成立,即
恒成立,即 ,
,令
 ,则
,则 ,
,∴
 ,
, ,…,
,…,
叠加得:
 …
… …
…

∴
 …
… ∴
∴ 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 本小题共13分)
本小题共13分)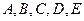 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.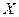 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加 课程的人数,求
课程的人数,求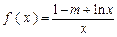 ,
,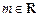 .
.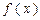 的极值;
的极值;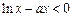 在
在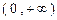 上恒成立,求
上恒成立,求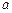 的取值范围.
的取值范围.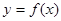 的定义域为R+,若对于给定的正数K,定义函数
的定义域为R+,若对于给定的正数K,定义函数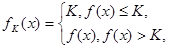 ,则当函数
,则当函数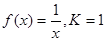 时,定积分
时,定积分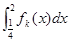 的值为
的值为 是定义在R上的函数,且
是定义在R上的函数,且

 ;
; .
. 在区间
在区间 内单调递增,则
内单调递增,则 的取值范围是____________.
的取值范围是____________. 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则点
,则点



 的图象经过点(4,
的图象经过点(4, 2),则函数
2),则函数 的值是( )
的值是( )
