Question

在△ABC中，B=45°，BC=3

2

，cosA=

10

10

．
（1）求AB的值；
（2）求BC边上的中线长．

Answer 1

考点：余弦定理,正弦定理

专题：解三角形

分析：（1）由cosA的值求出sinA的值，再由sinB以及BC的长，利用正弦定理求出AC的长，利用余弦定理即可求出AB的长；
（2）利用余弦定理求出BC边上的中线即可．

解答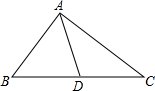： 解：（1）∵在△ABC中，B=45°，BC=3

2

，cosA=

10

10

，
∴sinB=

2

2

，sinA=

1-cos2A

=

3 10

10

，
由正弦定理

BC

sinA

=

AC

sinB

得：AC=

BCsinB

sinA

=

3 2 × 2 2

3 10 10

=

10

，
∴由余弦定理得：BC²=AC²+AB²-2AC•AB•cosA，即18=10+AB²-2AB，
解得：AB=4（负值舍去）；
（2）在△ABD中，AB=4，BD=

1

2

BC=

3 2

2

，B=45°，
由余弦定理得：AD²=AB²+BD²-2AB•BD•cosB=16+

9

2

-12=

17

2

，
则BC边上的中线AD长为

34

2

．

点评：此题考查了正弦、余弦定理，熟练掌握定理是解本题的关键．