题目内容
设矩阵M是把坐标平面上的点的纵坐标伸长到原来的2倍，横坐标保持不变的伸缩变换．
（Ⅰ）求矩阵M；
（Ⅱ）求矩阵M的特征值以及属于每个特征值的一个特征向量．
（Ⅰ）求矩阵M；
（Ⅱ）求矩阵M的特征值以及属于每个特征值的一个特征向量．
（Ⅰ）由条件得矩阵
（Ⅱ）
是矩阵M属于特征值
的一个特征向量，
是矩阵M属于特征值
的一个特征向量．
（Ⅱ）是矩阵M属于特征值的一个特征向量，是矩阵M属于特征值 的一个特征向量．(1)易求.
(2)由矩阵M，可知其特征多项式为
,然后利用
,可解出
的特征值，有两个值，然后分别求其特征向量即可
（Ⅱ）因为矩阵的特征多项式为，
令，解得特征值为，，
设属于特征值
的矩阵M的一个特征向量为
，则
，解得
，取
，得， 同理，对于特征值
，解得
，取
，得， 6分
所以是矩阵M属于特征值的一个特征向量，是矩阵M属于特征值 的一个特征向量．
.(2)由矩阵M，可知其特征多项式为
,然后利用,可解出的特征值，有两个值，然后分别求其特征向量即可（Ⅱ）因为矩阵
的特征多项式为，令
，解得特征值为，，设属于特征值
的矩阵M的一个特征向量为，则，解得，取，得， 同理，对于特征值，解得，取，得， 6分所以
是矩阵M属于特征值的一个特征向量，是矩阵M属于特征值 的一个特征向量．
练习册系列答案
相关题目
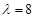及对应的一个特征向量
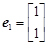，并且矩阵M对应的变换将点
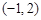变换成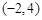
,求矩阵M．.
， 元素
的代数余子式为
，
， 
；
的定义域为
若
求实数
的取值范围；
，则行列式
．
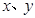的二元一次线性方程组的增广矩阵为
，记
，则此线性方程组有无穷多组解的充要条件是
． 
两两平行．
．
,则符合条件
的复数
的虚部为（ ） 
，如
，已知
，
，则
（ ）.
，
的方程。