题目内容

四棱柱ABCD-A1B1C1D1的底面ABCD为矩形，AB=1，AD=2，AA1=3，∠A1AB=∠A1AD=60°，则AC1的长为（　　）
A、4
2
B、23
C、
23
D、32
分析：记A1在面ABCD内的射影为O，O在∠BAD的平分线上，说明∠BAD的平分线即菱形ABCD的对角线AC，求AC1的长．
解答：精英家教网解：记A1在面ABCD内的射影为O，
∵∠A1AB=∠A1AD，
∴O在∠BAD的平分线上，
由O向AB，AD两边作垂线，垂足分别为E，F，连接A1E，A1F，A1E，A1F分别垂直AB，AD于E，F
∵AA1=3，∠A1AB=∠A1AD=60°，
∴AE=AF=
3
2

又四棱柱ABCD-A1B1C1D1的底面ABCD为矩形
∴∠OAF=∠OAE=45°，且OE=OF=
3
2
，可得OA=
3
2
2

在直角三角形A1OA中，由勾股定理得A1O=
3
2
2

过C1作C1M垂直底面于M，则有△C1MC≌△A1OA，由此可得M到直线AD的距离是
5
2
，M到直线AB的距离是
7
2
，C1M=A1O=
3
2
2

所以AC1 =
(
5
2
)2+(
7
2
)2+(
3
2
2
)2
=
23

故选C．
点评：本题考查棱柱的结构特征等知识，考查化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．解题关键在于，正确解三角形．
练习册系列答案
相关题目
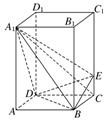精英家教网如图，在直四棱柱ABCD-A1B1C1D1中，AB=AD=2，DC=2
3
，AA1=
3
，AD⊥DC，AC⊥BD垂足为E．
（Ⅰ）求证BD⊥A1C；
（Ⅱ）求二面角A1-BD-C1的大小；
（Ⅲ）求异面直线AD与BC1所成角的大小．
精英家教网如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形，侧棱与底边长均为a，且∠A1AD=∠A1AB=60°．
①求证四棱锥A1-ABCD为正四棱锥；
②求侧面A1ABB1与截面B1BDD1的锐二面角大小．
精英家教网如图，正四棱柱ABCD-A1B1C1D1中，AA1=2AB=4，点E在CC1上，且CE=λCC1．
（1）λ为何值时，A1C⊥平面BED；
（2）若A1C⊥平面BED，求二面角A1-BD-E的余弦值．
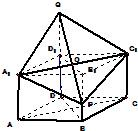精英家教网如图，已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形，Q是侧棱DD1（DD1＞
2
2
）延长线上的一点，过点Q、A1、C1作菱形截面QA1PC1交侧棱BB1于点P．设截面QA1PC1的面积为S1，四面体B1-A1C1P的三侧面△B1A1C1、△B1PC1、△B1A1P面积的和为S2，S=S1-S2．
（Ⅰ）证明：AC⊥QP；
（Ⅱ）当S取得最小值时，求cos∠A1QC1的值．
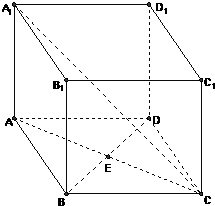精英家教网如图，直四棱柱ABCD-A1B1C1D1中，AB=AD=2，CB=CD=2 
3
，AA1=
3
，AB⊥BC，AC与BD交于点E．
（1）求证：BD⊥A1C；
（2）求二面角A1-BD-C1的大小；
（3）求异面直线AD与BC所成角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网