题目内容
【题目】抛物线
的焦点为F，斜率为正的直线l过点F交抛物线于A、B两点，满足
．
(1)求直线l的斜率；
(2)设点
在线段
上运动，原点
关于点的对称点为
，求四边形
的面积的最小值．
【答案】(1)
； (2) 
【解析】
（1）依题意
，设直线
方程为
，代入抛物线方程，由韦达定理知：
，
，由
，
，联立求解
，即可求出直线l的斜率。
（2）由(1)知：
四边形
的面积等于
，又
代入化简可得
，即可求出四边形的面积的最小值。
（1）依题意，设直线方程为，
则
，消去
得
，
设
，
，由韦达定理可得
，，①
，
因为，所以，②
联立①和②，消去
得
，
所以直线l的斜率是
（2）
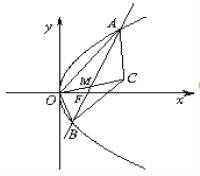
由点
与原点
关于点
对称，得是线段
的中点，从而点与点到直线l的距离相等，所以四边形的面积等于，
因为
所以
，四边形的面积的最小值．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
