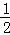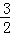题目内容
设函数fn(x)=-2n+
+
+…+
.
(1)求函数f2(x)在
上的值域;
(2)证明对于每一个n∈N*,在
上存在唯一的xn,使得fn(xn)=0;
(3)求f1(a)+f2(a)+…+fn(a)的值.
| 2 |
| x |
| 22 |
| x2 |
| 2n |
| xn |
(1)求函数f2(x)在
|
(2)证明对于每一个n∈N*,在
|
(3)求f1(a)+f2(a)+…+fn(a)的值.
(1)f2(x)=-4+
+
,
由x∈
,令t=
∈
,则y=4t2+2t-4.
对称轴t=-
,∴y=4t2+2t-4在
上单调递增,∴f2(x)在
上的值域为
.…(4分)
(2)证明:∵对于1≤x1<x2≤2,m∈N*有1≤
<
,
<
,从而
<
,∴y=
,m∈N*,在x∈
上单调递减,
∴fn(x)=-2n+
+
+…+
,在x∈
上单调递减.
又fn(1)=-2n+2+22+…+2n=2n-2≥0,fn(2)=-2n+n.…(7分)
当n≥2时,fn(2)=-2n+n=-(1+1)n+n=-
-
-
-…-
+n<0,
又f1(2)=-2+1=-1<0,即对于任意自然数n有fn(2)=-2n+n<0,
∴对于每一个n∈N*,存在唯一的xn∈
,使得fn(xn)=0…(11分)
(3)fm(a)=-2m+
+
+…+
.
当a=2时,fm(a)=-2m+m,∴f1(a)+f2(a)+…+fn(a)=-2n+1+
+2.…(14分)
当a≠2且a≠0时,fm(a)=-2m+
+
+…+
=-2m+
.
∴f1(a)+f2(a)+…+fn(a)=-2n+1+2+
-
+
…(18分)
| 2 |
| x |
| 4 |
| x2 |
由x∈
|
| 1 |
| x |
|
对称轴t=-
| 1 |
| 4 |
|
|
|
(2)证明:∵对于1≤x1<x2≤2,m∈N*有1≤
| x | m1 |
| x | m2 |
| 1 | ||
|
| 1 | ||
|
| 2m | ||
|
| 2m | ||
|
| 2m |
| xm |
|
∴fn(x)=-2n+
| 2 |
| x |
| 22 |
| x2 |
| 2n |
| xn |
|
又fn(1)=-2n+2+22+…+2n=2n-2≥0,fn(2)=-2n+n.…(7分)
当n≥2时,fn(2)=-2n+n=-(1+1)n+n=-
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
又f1(2)=-2+1=-1<0,即对于任意自然数n有fn(2)=-2n+n<0,
∴对于每一个n∈N*,存在唯一的xn∈
|
(3)fm(a)=-2m+
| 2 |
| a |
| 22 |
| a2 |
| 2m |
| am |
当a=2时,fm(a)=-2m+m,∴f1(a)+f2(a)+…+fn(a)=-2n+1+
| n(n+1) |
| 2 |
当a≠2且a≠0时,fm(a)=-2m+
| 2 |
| a |
| 22 |
| a2 |
| 2m |
| am |
| ||||
1-
|
∴f1(a)+f2(a)+…+fn(a)=-2n+1+2+
| 2n |
| a-2 |
| 4 |
| (a-2)2 |
| 2n+2 |
| (a-2)2an |

练习册系列答案
相关题目
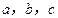 求证:
求证: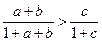
 为正整数,且
为正整数,且 与
与 皆为完全平方数,对于以下两个命题:
皆为完全平方数,对于以下两个命题:
 必为合数;(乙).
必为合数;(乙). 必为两个平方数的和.
必为两个平方数的和. 为实数时,则实数
为实数时,则实数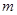 的值是_________.
的值是_________. 的点位于
的点位于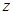 满足
满足 ,则
,则 等于( )
等于( )



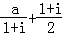 是实数,则a=( )
是实数,则a=( )