题目内容

在四边形ABCD中，
AB
=
DC
=（1，0），
BA
|
BA|
+
BC
|
BC
|
=
BD
|
BD
|
，则四边形ABCD的面积是（　　）
A、
3
2
B、
3
C、
3
4
D、
3
2
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：根据题意，先判断四边形ABCD是平行四边形，再判断平行四边形ABCD是菱形，求出它的面积即可．
解答： 解：在四边形ABCD中，
AB
=
DC
=（1，0），∴四边形ABCD是平行四边形；
又∵
BA
|
BA|
+
BC
|
BC
|
=
BD
|
BD
|
，
∴平行四边形ABCD的角平分线BD平分∠ABC，四边形ABCD是菱形，其边长为1，对角线BD等于1，
∴cos∠ABC=cos120°=-
1
2
，如图所示；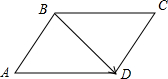
∴sin∠ABC=
3
2
，
SABCD=2×
1
2
|
BA
|•|
BC
|•sin∠ABC=2×
1
2
×1×1×
3
2
=
3
2
．
故选：A．
点评：本题考查了平面向量的应用问题，解题时应先判断四边形的形状，是基础题．
练习册系列答案
相关题目
设函数f（x）=ax-（k-1）a-x（a＞0且a≠1）是定义域为R的奇函数．
（Ⅰ）求k值；
（Ⅱ）若f（1）＜0，求使不等式f（x2+tx）+f（4-x）＜0恒成立的实数t的取值范围；
（Ⅲ）若f（1）=
3
2
，且g（x）=a2x+a-2x-2mf（x）在[1，+∞）上的最小值为-2，求实数m的值．
已知f（x）定义在区间（0，+∞）上的减函数，且满足f（x•y）=f（x）+f（y），并且f(
1
3
)=1
（1）求f（1）
（2）求f(
1
9
)
（3）若f（x）+f（1-2x）＜2，求x的范围．
已知函数f（x）=cos（2x+
π
3
），若函数g（x）的最小正周期是π，且当x∈[-
π
2
，
π
2
]时g（x）=f（
x
2
），则关于x的方程g（x）=
3
2
的解集为
 
．
直线y=x与椭圆
x2
4
+y2=1相交于A，B两点，则|AB|=（　　）
A、2
B、
4
5
5
C、
4
10
5
D、
8
10
5
甲、乙两人参加某种选拔测试．在备选的5道题中，甲能答对其中的2道题，乙能答对其中的3道题．规定每次考试都从备选的5道题中随机抽出3道题进行测试，答对一题加10分，答错一题（不答视为答错）减5分，至少得15分才能入选．
（Ⅰ）求乙得15分的概率；
（Ⅱ）求甲入选的概率和乙入选的概率．
函数f（x）=sin（-2x+
π
3
）的最小正周期是
 
．
已知向量
m
=（ex，lnx+k），
n
=（1，f（x）），
m
∥
n
（k为常数，e是自然对数的底数），曲线y=f（x）在点（1，f（1））处的切线与y轴垂直，F（x）=xexf′（x）．
（1）求k的值；
（2）求F（x）的单调区间及最大值．
已知角θ的顶点与原点重合，始边与x轴的正半轴重合，角θ的正弦线长为
3
2
，则cos2θ=（　　）
A、-
1
2
B、
2
5
C、
1
2
D、
1
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网