题目内容
椭圆C: 的左、右焦点分别为F1(-1,0)、F2(1,0),O是坐标原点,C的右顶点和上顶点分别为A、B,且△AOB的面积为
的左、右焦点分别为F1(-1,0)、F2(1,0),O是坐标原点,C的右顶点和上顶点分别为A、B,且△AOB的面积为 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点P(4,0)作与x轴不重合的直线l与C交于相异两点M、N,交y轴于Q点,证明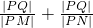 为定值,并求这个定值.
为定值,并求这个定值.
(Ⅰ)解:依题意得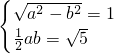 …(3分)
…(3分)
解得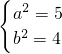 ,故椭圆C的方程为
,故椭圆C的方程为 . …(5分)
. …(5分)
(Ⅱ)证明:依题意可设直线l的方程为x=ky+4…(6分)
由 ,消去x可得(4k2+5)y2+32ky+44=0
,消去x可得(4k2+5)y2+32ky+44=0
设M(x1,y1),N(x2,y2),Q(0,y3),则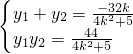 …(8分)
…(8分)
又由直线l的方程x=ky+4知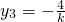
由三角形的相似比得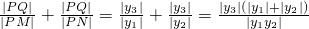
注意到y1y2>0,
∴|y1|+|y2|=|y1+y2|
∴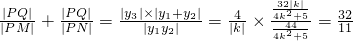
故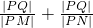 为定值
为定值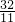 . …(12分)
. …(12分)
分析:(Ⅰ)利用椭圆的左、右焦点分别为F1(-1,0)、F2(1,0),O是坐标原点,C的右顶点和上顶点分别为A、B,且△AOB的面积为 ,建立方程组,即可求得椭圆C的方程;
,建立方程组,即可求得椭圆C的方程;
(Ⅱ)设直线l的方程,代入椭圆方程,可得一元二次方程,利用韦达定理,及三角形的相似比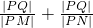 ,即可证得结论.
,即可证得结论.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,联立方程,正确表示比值是关键.
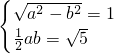 …(3分)
…(3分)解得
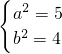 ,故椭圆C的方程为
,故椭圆C的方程为 . …(5分)
. …(5分)(Ⅱ)证明:依题意可设直线l的方程为x=ky+4…(6分)
由
 ,消去x可得(4k2+5)y2+32ky+44=0
,消去x可得(4k2+5)y2+32ky+44=0设M(x1,y1),N(x2,y2),Q(0,y3),则
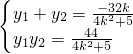 …(8分)
…(8分)又由直线l的方程x=ky+4知
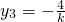
由三角形的相似比得
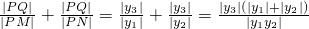
注意到y1y2>0,
∴|y1|+|y2|=|y1+y2|
∴
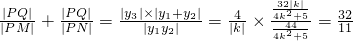
故
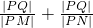 为定值
为定值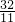 . …(12分)
. …(12分)分析:(Ⅰ)利用椭圆的左、右焦点分别为F1(-1,0)、F2(1,0),O是坐标原点,C的右顶点和上顶点分别为A、B,且△AOB的面积为
 ,建立方程组,即可求得椭圆C的方程;
,建立方程组,即可求得椭圆C的方程;(Ⅱ)设直线l的方程,代入椭圆方程,可得一元二次方程,利用韦达定理,及三角形的相似比
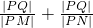 ,即可证得结论.
,即可证得结论.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,联立方程,正确表示比值是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,P是C上的点,
,P是C上的点, ⊥
⊥ =
= ,则C的离心率为( )
,则C的离心率为( )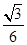 B.
B. C.
C. D.
D.
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,点
,点 满足
满足
 ;
; ,设直线
,设直线 与椭圆C相交于A,B两点,且
与椭圆C相交于A,B两点,且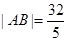 ,
,