题目内容
如图所示,己知 为
为 的
的 边上一点,
边上一点, 经过点
经过点 ,交
,交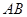 于另一点
于另一点 ,
, 经过点
经过点 ,
, ,交
,交 于另一点
于另一点 ,
, 与
与 的另一交点为
的另一交点为 .
.
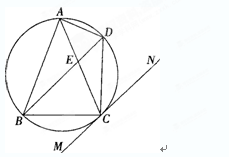
(I)求证: 四点共圆;
四点共圆;
(II)若 切
切 于
于 ,求证:
,求证: .
.
(I) 四点共圆;(II)
四点共圆;(II) .
.
解析试题分析:(I)要证 四点共圆,只需找出四边形
四点共圆,只需找出四边形 中一组对角之和为
中一组对角之和为 ,连接
,连接 ,则四边形
,则四边形 分别内接于
分别内接于 ,则
,则 ,而
,而 ,故
,故 ,从而
,从而 四点共圆;(II)要证明
四点共圆;(II)要证明 ,需要根据题中给定的角度相关关系解决,由(1)知
,需要根据题中给定的角度相关关系解决,由(1)知 四点共圆,根据同弧所对的圆周角相等,则
四点共圆,根据同弧所对的圆周角相等,则 ,而
,而 切
切 于
于 ,则弧
,则弧 所对的角
所对的角 与弦切角
与弦切角 相等,故
相等,故 ,得证.
,得证.
试题解析:证明:(I)如图,连接 ,四边形
,四边形 分别内接于
分别内接于 ,
, ,又
,又 ,
, ,所以
,所以 四点共圆;
四点共圆;
(II) 四点共圆,
四点共圆, ,因为
,因为 切
切 于
于 ,
, ,所以
,所以 ,得证.
,得证.
考点:1.四点共圆的证明;2.圆的平面几何性质应用.

练习册系列答案
相关题目

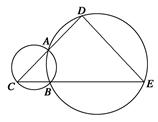
 与⊙
与⊙ 相切,
相切, 为切点,
为切点, 为割线,弦
为割线,弦 ,
, 相交于
相交于 点,
点, 为
为 上一点,且
上一点,且 .
.
 ;
; .
. 为△
为△ 外接圆的切线,
外接圆的切线,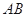 的延长线交直线
的延长线交直线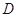 ,
,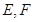 分别为弦
分别为弦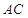 上的点,且
上的点,且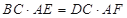 ,
,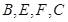 四点共圆.
四点共圆. 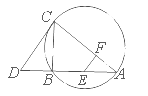
 是△
是△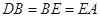 ,求过
,求过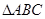 中,
中,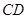 是
是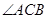 的角平分线,
的角平分线, 的外接圆交
的外接圆交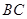 于
于 ,
,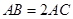 .
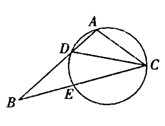
.
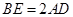 ;
;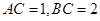 时,求
时,求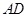 的长.
的长.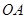 、
、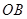 是圆
是圆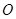 的半径,且
的半径,且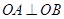 ,
,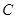 是半径
是半径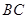 交圆
交圆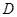 ,过
,过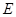 .求证:
.求证: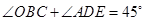 .
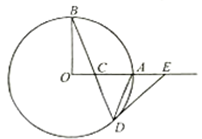
.
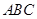 内接于⊙
内接于⊙ ,
,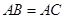 ,直线
,直线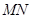 切⊙
切⊙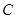 ,弦
,弦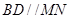 ,
, 相交于点
相交于点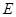 .
.
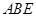 ≌△
≌△ ;
;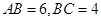 ,求
,求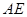 长.
长.