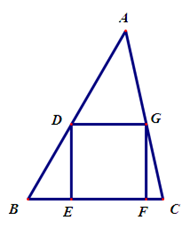
题目内容
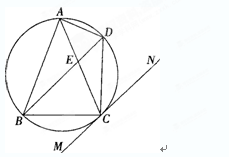
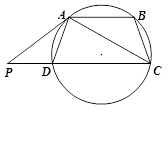
如图,△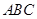 内接于⊙
内接于⊙ ,
,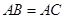 ,直线
,直线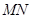 切⊙
切⊙ 于点
于点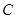 ,弦
,弦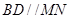 ,
, 相交于点
相交于点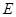 .
.
(Ⅰ)求证:△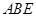 ≌△
≌△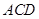 ;
;
(Ⅱ)若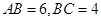 ,求
,求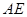 长.
长.
(Ⅰ) 证明详见解析;(Ⅱ) 
解析试题分析:(1)利用弦切角定理和平行线,证明∠BAE=∠CAD,而已知AB="AC," ∠ABE=∠ACD,即可证△ABE≌△ACD.(2) 由平行线和弦切角定理可证∠BDC=∠EBC,所以BC=CD=4,再利用教的等量代换证∠ABC=∠ACB,所以BC=BE=4,利用圆周角的性质可得证明△ABE∽△DEC的条件,最后由三角形的相似比即可求出AE的长.
试题解析:(1)在 △
△ 和△
和△ 中
中 


 ∥
∥

 直线是圆的切线
直线是圆的切线 

 △
△ ≌△
≌△
(2)




又

设 △
△ ∽△
∽△


又



考点:1.弦切角定理及平行线;2.圆周角和全等三角形;3.相似三角形及其性质.

练习册系列答案
相关题目

 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径. 为
为 的
的 边上一点,
边上一点, 经过点
经过点 ,交
,交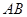 于另一点
于另一点 ,
, 经过点
经过点 ,
, 于另一点
于另一点 ,
, .
.
 四点共圆;
四点共圆; 切
切 .
. 为圆
为圆 的直径,
的直径, 为垂直于
为垂直于 ,弦
,弦 与
与 .
.
 四点共圆;
四点共圆; .
.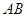 是
是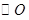 的直径,弦
的直径,弦 与
与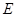 ,点
,点 为弦
为弦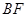 、
、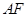 并延长交
并延长交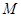 、
、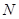 .
. 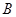 、
、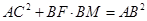 .
.
 :
: .
.
 是圆的内接四边形,
是圆的内接四边形, ,过
,过 点的圆的切线与
点的圆的切线与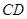 的延长线交于
的延长线交于 点,证明:
点,证明: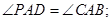
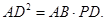
 、
、 分别与圆
分别与圆 相切于
相切于 、
、 ,
, 经过圆心
经过圆心 ,求证:
,求证: .
.