题目内容
求曲线y=
(0≤x≤4)上的一条切线,使此切线与直线x=0,x=4以及曲线y=
所围成的平面图形的面积最小.
| x |
| x |
设(x0,y0)为曲线y=
(0≤x≤4)上任一点,得曲线于该点处的切线方程为:y-y0=
(x-x0)即y=
+
.
得其与x=0,x=4的交点分别为(0,
),(4,
+
)
于是由此切线与直线x=0,x=4以及曲线y=
所围的平面图形面积为:S=
(
+
-
)dx=2y0+
-
=2
+
-
应用均值不等式求得x0=2时,S取得最小值.
即所求切线即为:y=
+
.
| x |
| 1 | ||
2
|
| y0 |
| 2 |
| x | ||
2
|
得其与x=0,x=4的交点分别为(0,
| y0 |
| 2 |
| y0 |
| 2 |
| 2 |
| y0 |
于是由此切线与直线x=0,x=4以及曲线y=
| x |
| ∫ | 40 |
| y0 |
| 2 |
| x | ||
2
|
| x |
| 4 | ||
|
| 16 |
| 3 |
| x0 |
| 4 | ||
|
| 16 |
| 3 |
应用均值不等式求得x0=2时,S取得最小值.
即所求切线即为:y=
| x | ||
2
|
| ||
| 2 |

练习册系列答案
相关题目


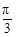 ,k∈Z}
,k∈Z}