题目内容
已知un=an-1b+an-2b2+…+abn-1+bn(n∈N*,a>0,b>0).
(Ⅰ)当a=b时,求数列{un}的前项n项和Sn。
(Ⅱ)求
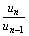 。
。

(Ⅱ)由(Ⅰ),当a=b时,un=(n+1)an,则
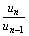 =
=
 =
=
 =a.
=a.
当a≠b时,un=an+an-1b+…+abn-1+bn=an[1+ ]
]
=
或a>b>0, 
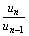 =
=
 =
=

若b>a>0, 
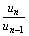 =
=
 。
。

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
已知un=an-1b+an-2b2+…+abn-1+bn(n∈N*,a>0,b>0).
(Ⅰ)当a=b时,求数列{un}的前项n项和Sn。
(Ⅱ)求
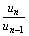 。
。

(Ⅱ)由(Ⅰ),当a=b时,un=(n+1)an,则
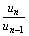 =
=
 =
=
 =a.
=a.
当a≠b时,un=an+an-1b+…+abn-1+bn=an[1+ ]
]
=
或a>b>0, 
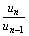 =
=
 =
=

若b>a>0, 
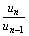 =
=
 。
。

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案