题目内容
设f(x)=ax2+bx,1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范围.
【解析】方法1:设f(-2)=mf(-1)+nf(1) (m,n为待定系数),
则4a-2b=m(a-b)+n(a+b),即4a-2b=(m+n)a+(n-m)b.
于是得 ,解得
,解得 ,∴f(-2)=3f(-1)+f(1).
,∴f(-2)=3f(-1)+f(1).
又∵1≤f(-1)≤2,2≤f(1)≤4,∴5≤3f(-1)+f(1)≤10,故5≤f(-2)≤10.
方法2:由 ,得
,得 ,∴f(-2)=4a-2b=3f(-1)+f(1).
,∴f(-2)=4a-2b=3f(-1)+f(1).
又∵1≤f(-1)≤2,2≤f(1)≤4,∴5≤3f(-1)+f(1)≤10,∴5≤f(-2)≤10.

练习册系列答案
相关题目
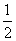 .
.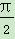 ,且sin α=
,且sin α=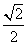 ,求f(α)的值;
,求f(α)的值;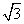 ≈1.73)
≈1.73)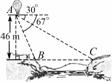 图13
图13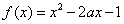 ,当
,当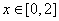 上有最小值
上有最小值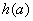 ,最大值为
,最大值为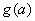
 ,
, 的最小值为
的最小值为 ,求
,求 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围
的取值范围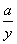 >
>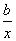 这五个式子中,恒成立的所有不等式的序号是________.
这五个式子中,恒成立的所有不等式的序号是________. 求这个二次函数的解析式,并写出函数的值域和单调区间?
求这个二次函数的解析式,并写出函数的值域和单调区间?
 B.必要不充分条件
B.必要不充分条件 D.既不充分也不必要条件
D.既不充分也不必要条件