题目内容
设集合M={x|-2<x<5},N={x|2-t<x<2t+1,t∈R},若M∩N=N,则实数t的取值范围是 .
考点:交集及其运算
专题:集合
分析:由M∩N=N得N⊆M,对集合N分两种情况分别求出实数t的取值范围,最后在并在一起.
解答:
解:由M∩N=N得,N⊆M,
因为集合M={x|-2<x<5},N={x|2-t<x<2t+1,t∈R},
所以当N=∅时,有2-t≥2t+1,解得t≤
,
当N≠∅时,有
,解得
<t≤2,
综上得,实数t的取值范围是(-∞,2],
故答案为:(-∞,2].
因为集合M={x|-2<x<5},N={x|2-t<x<2t+1,t∈R},
所以当N=∅时,有2-t≥2t+1,解得t≤
| 1 |
| 3 |
当N≠∅时,有
|
| 1 |
| 3 |
综上得,实数t的取值范围是(-∞,2],
故答案为:(-∞,2].
点评:本题考查交集、并集的运算,以及集合之间的关系,考查了分类讨论思想,易忘的地方是空集.

练习册系列答案
相关题目
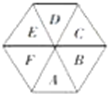 在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.
在一个正六边形的六个区域栽种观赏植物(如图),要求同一块中种同一种植物,相邻的两块种不同的植物.(1)现有2种不同的植物可供选择,则有种栽
(2)现有4种不同的植物可供选择,则有
命题:“若x>1,则lnx>0”的否命题为( )
| A、若x>1,则lnx≤0 |
| B、若x≤1,则lnx>0 |
| C、若x≤1,则lnx≤0 |
| D、若lnx>1,则x>0 |
下列角中,终边在y轴正半轴上的是( )
A、
| ||
B、
| ||
| C、π | ||
D、
|
为了解2000名学生对学校食堂的意见,准备从中抽取一个样本容量为50的样本.若采用系统抽样,则分段间隔k为( )
| A、20 | B、30 | C、40 | D、50 |
i是虚数单位,
=( )
| i |
| -1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|