题目内容
(本小题满分12分)已知函数 ,其中常数
,其中常数 .
.
(1)当 时,求函数
时,求函数 的极大值;
的极大值;
(2)试讨论 在区间
在区间 上的单调性;
上的单调性;
(3)当 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 ,
, ,使得曲线
,使得曲线 在点
在点 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.
(1)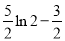 ;
;
(2)当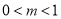 时,
时,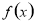 在
在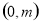 上单调递减,在
上单调递减,在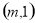 上单调递增,
上单调递增,
当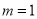 时,
时,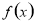 在
在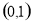 单调递减,当
单调递减,当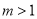 时,
时,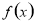 在
在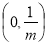 上单调递减,在
上单调递减,在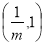 上单调递增;
上单调递增;
(3)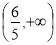 .
.
【解析】
试题分析:(1)求函数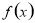 的极值的一般步骤:(1)确定函数的定义域;(2)求导数
的极值的一般步骤:(1)确定函数的定义域;(2)求导数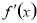 ;(3)解方程
;(3)解方程 ,求出函数定义域内的所有根;(4)列表检验
,求出函数定义域内的所有根;(4)列表检验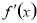 在
在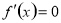 的根
的根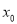 左右两侧的符号,如果在
左右两侧的符号,如果在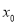 附近的左侧
附近的左侧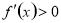 ,右侧
,右侧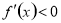 ,那么
,那么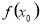 是极大值;如果在
是极大值;如果在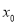 附近的左侧
附近的左侧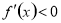 ,右侧
,右侧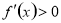 ,那么
,那么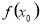 是极小值;(2)函数
是极小值;(2)函数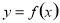 在某个区间内可导,则若
在某个区间内可导,则若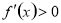 ,则
,则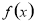 在这个区间内单调递增,若
在这个区间内单调递增,若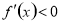 ,则
,则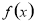 在这个区间内单调递减;(3)对于恒成立的问题,常用到两个结论:(1)
在这个区间内单调递减;(3)对于恒成立的问题,常用到两个结论:(1)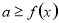 恒成立
恒成立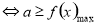 ,(2)
,(2)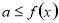 恒成立
恒成立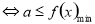 .
.
试题解析:(1)当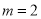 时,
时,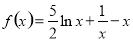 ,
,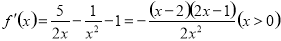 ,
,
由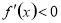 得
得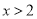 或
或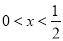 ,由
,由 得
得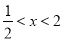 ,因此函数
,因此函数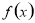 在区间
在区间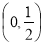 和
和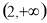 单调递减,在区间
单调递减,在区间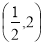 上单调递增,故
上单调递增,故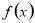 的极大值为
的极大值为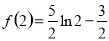

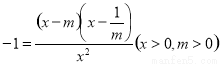
当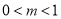 时,
时,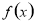 在
在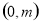 上单调递减,在
上单调递减,在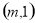 上单调递增
上单调递增
当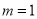 时,
时,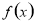 在
在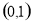 单调递减
单调递减
当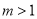 时,
时,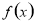 在
在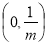 上单调递减,在
上单调递减,在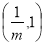 上单调递增
上单调递增
(3)由题意,可得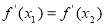 (
(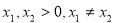 )
)
既
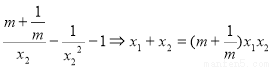
 对
对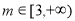 恒成立
恒成立
另 则
则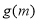 在
在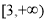 上单调递增,
上单调递增,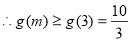
故 ,从而
,从而
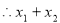 的取值范围是
的取值范围是 .
.
考点:1、利用导数求函数极值;2、利用导数求函数的单调性;3、恒成立的问题.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
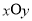 中,已知动点
中,已知动点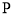 到两个定点
到两个定点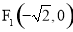 ,
,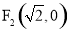 的距离的和为定值
的距离的和为定值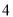 .
.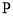 运动所成轨迹
运动所成轨迹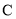 的方程;
的方程;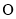 为坐标原点,若点
为坐标原点,若点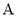 在轨迹
在轨迹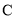 上,点
上,点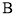 在直线
在直线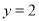 上,且
上,且 ,试判断直线
,试判断直线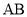 与圆
与圆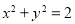 的位置关系,并证明你的结论.
的位置关系,并证明你的结论. 的实部是
的实部是 B.
B. C.
C. D.
D.
 所表示的平面区域为
所表示的平面区域为 ,若直线
,若直线 与平面区域
与平面区域 的取值范围为是
的取值范围为是 B.
B.
 D.
D.
 (
( 是虚数单位)的虚部是
是虚数单位)的虚部是 B.
B. C.
C. D.
D.
 存在垂直于
存在垂直于 轴的切线,且函数
轴的切线,且函数 在
在 上单调递减,则
上单调递减,则 的范围为 .
的范围为 . 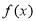 的定义域为
的定义域为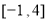 ,部分对应值如下表,
,部分对应值如下表,
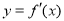 的图象如右图所示.当
的图象如右图所示.当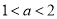 时,函数
时,函数 的零点的个数为( )
的零点的个数为( )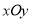 中,圆
中,圆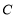 的方程为
的方程为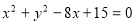 ,若直线
,若直线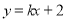 上至少存在一点,使得以该点为圆心,半径为
上至少存在一点,使得以该点为圆心,半径为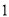 的圆与圆
的圆与圆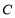 有公共点,则
有公共点,则 的最小值是____.
的最小值是____.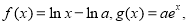 其中
其中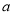 为常数,函数
为常数,函数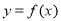 和
和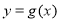 的图象在它们与坐标轴交点的切线互相平行.
的图象在它们与坐标轴交点的切线互相平行.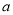 的值;
的值;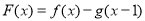 的单调区间;
的单调区间;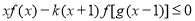 在区间
在区间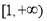 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.