题目内容
(本小题满分14分)已知函数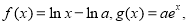 其中
其中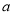 为常数,函数
为常数,函数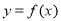 和
和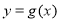 的图象在它们与坐标轴交点的切线互相平行.
的图象在它们与坐标轴交点的切线互相平行.
(Ⅰ)求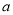 的值;
的值;
(Ⅱ)求函数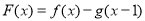 的单调区间;
的单调区间;
(Ⅲ)若不等式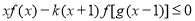 在区间
在区间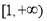 上恒成立,求实数
上恒成立,求实数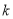 的取值范围.
的取值范围.
(1)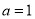 ;(2)单调递增区间为
;(2)单调递增区间为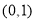 ,单调递减区间为
,单调递减区间为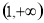 ;(3)
;(3)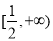 .
.
【解析】
试题分析:(1)利用导数的几何意义进行求解;(2)求导,利用导数的符号求函数的单调区间;(3)构造函数,将不等式恒成立问题转化为求函数的最值问题.
试题解析:(Ⅰ)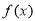 与坐标轴交点为
与坐标轴交点为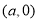 ,
,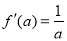 , 1分
, 1分
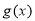 与坐标轴交点为
与坐标轴交点为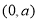 ,
,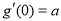 2分
2分
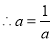 解得
解得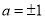 ,又
,又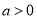 ,故
,故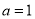 4分
4分
(Ⅱ)由(Ⅰ)知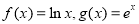 ,
,
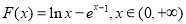
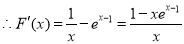 5分
5分
令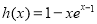 ,显然函数
,显然函数 在区间
在区间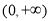 上单调递减,且
上单调递减,且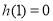 6分
6分
当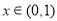 时,
时,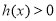 ,
,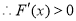 ,
,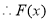 在
在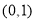 上单调递增
上单调递增
当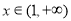 时,
时,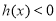 ,
,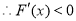 ,
,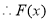 在
在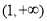 上单调递减 8分
上单调递减 8分
故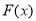 的单调递增区间为
的单调递增区间为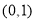 ,单调递减区间为
,单调递减区间为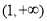 . 9分
. 9分
(2)原不等式等价于: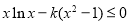 在区间
在区间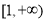 上恒成立.
上恒成立.
设
则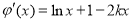 10分
10分
令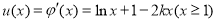
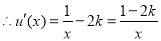 11分
11分
①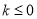 时,
时,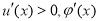 在区间
在区间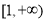 上单调递增,
上单调递增,
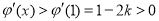
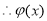 在
在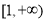 上单调递增,
上单调递增,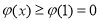
不符合题意,舍去. 12分
②当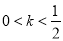 时,若
时,若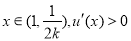
则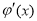 在
在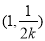 上单调递增,
上单调递增,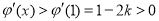
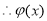 在
在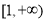 上单调递增,
上单调递增,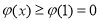
不符合题意,舍去. 13分
③当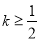 时,
时,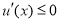 在
在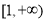 恒成立,
恒成立,
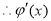 在
在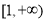 上单调递减
上单调递减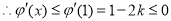
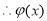 在
在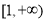 上单调递减
上单调递减
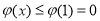 即
即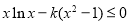 对
对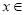
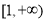 恒成立,
恒成立,
综上所述,实数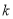 的取值范围是
的取值范围是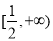 .
.
考点:1.导数的几何意义;2.函数的单调性;3.不等式恒成立问题.
考点分析: 考点1:导数及其应用 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 ,其中常数
,其中常数 .
. 时,求函数
时,求函数 的极大值;
的极大值; 上的单调性;
上的单调性; 时,曲线
时,曲线 上总存在相异两点
上总存在相异两点 ,
, ,使得曲线
,使得曲线 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.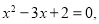 则
则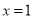 ”的逆否命题为“若
”的逆否命题为“若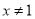 则
则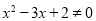 ”
”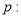 存在
存在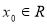 ,使得
,使得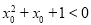 ,则非
,则非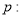 任意
任意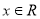 ,都有
,都有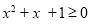
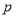 且
且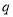 为假命题,则
为假命题,则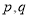 均为假命题
均为假命题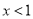 ”是“
”是“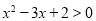 ”的充分不必要条件
”的充分不必要条件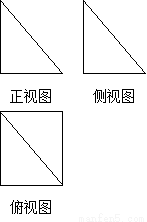
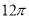 B.
B.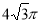 C.
C.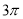 D.
D.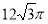
 ,
, ,若
,若 ,则
,则 的值为
的值为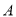 :
: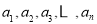
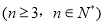 中,令
中,令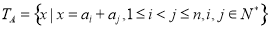 ,
,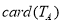 表示集合
表示集合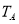 中元素的个数.若
中元素的个数.若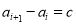 (
(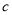 为常数,且
为常数,且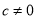 ,
,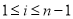 )则
)则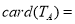 .
.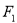 ,
,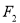 是双曲线
是双曲线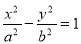
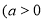 ,
,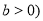 的左、右两个焦点,若双曲线右支上存在一点
的左、右两个焦点,若双曲线右支上存在一点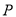 ,使
,使 (
(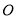 为坐标原点),且
为坐标原点),且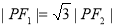 ,则双曲线的离心率为
,则双曲线的离心率为  B.
B.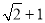 C.
C.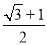 D.
D.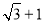
 ,则
,则 = .(结果用
= .(结果用 表示)
表示)
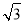 ,BC=1,AC=2,O为球心,则三棱锥O—ABC的体积为 .
,BC=1,AC=2,O为球心,则三棱锥O—ABC的体积为 .