题目内容
6.分别根据下列条件,求圆的方程:(1)过两点(0,4),(4,6),且圆心在直线x-2y-2=0上;
(2)半径为$\sqrt{13}$,且与直线2x+3y-10=0切于点(2,2).
分析 (1)由圆心在直线x-2y-2=0上,可设圆心坐标为(2b+2,b),再根据圆心到两点A(0,4)、B(4,6)的距离相等,求出b的值,可得圆心坐标和半径,从而求得圆的标准方程;
(2)设圆心坐标为(x,y),利用半径为$\sqrt{13}$,且与直线2x+3y-10=0切于点P(2,2),建立方程组,求出圆心坐标,即可求得圆的方程.
解答 解:(1)由于圆心在直线x-2y-2=0上,可设圆心坐标为(2b+2,b),
再根据圆过两点A(0,4),B(4,6),可得[(2b+2)-0]2+(b-4)2=[(2b+2)-4]2+(b-6)2,
解得b=1,可得圆心为(4,1),半径为$\sqrt{(4-0)^{2}+(1-4)^{2}}$=5,
故所求的圆的方程为(x-4)2+(y-1)2=25;
(2)设圆心坐标为(x,y),则$\left\{\begin{array}{l}{\frac{y-2}{x-2}•(-\frac{2}{3})=-1}\\{(x-2)^{2}+(y-2)^{2}=13}\end{array}\right.$,
∴x=0,y=-1或x=1.8,y=5.6,
∴圆的方程为(x-4)2+(y-5)2=13或x2+(y+1)2=13
点评 本题主要考查圆的标准方程的求法,求出圆心的坐标,是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.cos70°sin80°+cos20°sin10°=( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
17.复数z满足z=$\frac{2-i}{1-i}$,则z=( )
| A. | 1+3i | B. | 3-i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$+$\frac{3}{2}$i |
11.已知函数y=ax2+bx+c,其中a,b,c∈{0,1,2},则不同的二次函数的个数共有( )
| A. | 256个 | B. | 18个 | C. | 16个 | D. | 10个 |
18.已知X的分布列如表:
且b2=ac,$a=\frac{1}{2}$,则E(X)=( )
| X | -1 | 0 | 1 | 2 |
| P | a | b | c | $\frac{5}{18}$ |
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
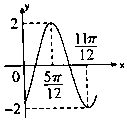 函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则ω=2,φ=-$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则ω=2,φ=-$\frac{π}{3}$.