题目内容
在 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且 .
.
(1).求角B的大小;
(2).求sin A+sin C的取值范围.
 分别是角A、B、C的对边,
分别是角A、B、C的对边, ,且
,且 .
.(1).求角B的大小;
(2).求sin A+sin C的取值范围.
(1)B= ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)由
 ,可得
,可得 ,等式中边角混在了一起,需要进行边角的统一,根据正弦定理可得
,等式中边角混在了一起,需要进行边角的统一,根据正弦定理可得 ,进一步变形化简可得
,进一步变形化简可得 ,∴B
,∴B ;(2)由(1)可得
;(2)由(1)可得 ,即
,即 ,因此可以将sinA+sinC进行三角恒等变形转化为关于A的函数,即
,因此可以将sinA+sinC进行三角恒等变形转化为关于A的函数,即
 ,从而可以得到sinA+sinC取值范围是
,从而可以得到sinA+sinC取值范围是 .
.(1) 由
 ,得
,得

由正弦定理得:
 ,
, 又
又

又
 又
又 ;
; ∵
 ,∴
,∴ ,
,∴

 ,
,∵
 ,∴
,∴ ,∴
,∴ ,∴
,∴ .
.故sin A+sin C的取值范围是
 .
. 
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 中,角
中,角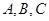 所对的边分别为
所对的边分别为 ,且满足
,且满足 .
. ,
, ,求
,求 的长.
的长. 的内角
的内角 所对边的长分别是
所对边的长分别是 ,且
,且
 的值;
的值; 的值.
的值. 中,
中, ,
, ,
, ,点
,点 是
是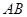 的中点.
的中点.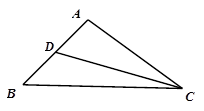
 的值和中线
的值和中线 的长
的长 中,内角
中,内角 所对边长分别为
所对边长分别为 ,
, ,
, .
. ;
; .
.




 中三个内角 A、B、C所对的边分别为
中三个内角 A、B、C所对的边分别为 则下列判断错误的是( )
则下列判断错误的是( ) 则
则 则
则 则
则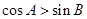 则
则 ,则sinB=( )
,则sinB=( )

