题目内容

6．从装有2个红球和2个黑球的口袋内任取2个球，则与事件恰有两个红球既不对立也不互斥的事件是（　　）
A．至少有一个黑球B．恰好一个黑球C．至多有一个红球D．至少有一个红球

分析 利用对立事件、互斥事件定义直接求解．

解答 解：从装有2个红球和2个黑球的口袋内任取2个球，
在A中，至少有一个黑球与事件恰有两个红球是对立事件，故A不成立；
在B中，恰好一个黑球与事件恰有两个红球是互的事件，故B不成立；
在C中，至多一个红球与事件恰有两个红球是对立事件，故C不成立；
在D中，至少一个红球与事件恰有两个红球既不对立也不互斥的事件，故D成立．
故选：D．

点评 本题考查既不对立也不互斥的事件的判断，是基础题，解题时要认真审题，注意对立事件、互斥事件的定义的合理运用．

练习册系列答案
相关题目
16．函数$f（x）=（{1-\frac{2}{{1+{2^x}}}}）tanx$的图象（　　）
A．关于x轴对称B．关于y轴对称C．关于y=x轴对称D．关于原点轴对称
17．已知等比数列{an}中，各项都是正数，且3a1，$\frac{1}{2}$a3，2a2成等差数列，则等比数列{an}公比q等于（　　）
A．3B．9C．27D．81
14．不等式组$\left\{\begin{array}{l}{2x-y+1≥0}\\{x-2y+2≤0}\\{x+y-4≤0}\end{array}\right.$的解集记作D，实数x，y满足如下两个条件：①?（x，y）∈D，y≥ax；②?（x，y）∈D，x-y≤a．则实数a的取值范围为[-2，1]．
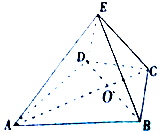1．如图，在四棱锥E-ABCD中，△ABD是正三角形，△BCD是等腰三角形，∠BCD=120°，EC⊥BD．
（Ⅰ）求证：BE=DE；
（Ⅱ）若AB=2$\sqrt{3}$，AE=3$\sqrt{2}$，平面EBD⊥平面ABCD，直线AE与平面ABD所成的角为45°，求二面角B-AE-D的余弦值．
11．从集合{1，2，3，4}中任取两个不同的数，则这两个数的和为3的倍数的槪率为$\frac{1}{3}$．
18．如图，在几何体A1B1D1-ABCD中，四边形A1B1BA与A1D1DA均为直角梯形，且AA1⊥底面ABCD，四边形ABCD为正方形，AB=2A1D1=2A1B1=4，AA1=4，P为DD1的中点．
（Ⅰ）求证：AB1⊥PC；
（Ⅱ）求平面B1CD1与平面PBC所成的锐二面角的余弦值．
8．（1）曲线C：$\frac{x^2}{4-k}-\frac{y^2}{1-k}=1$表示焦点在x轴上的椭圆，则k的范围；
（2）求以F1（-2，0），F2（2，0）为焦点，且过点$M（\sqrt{6}，2）$的椭圆标准方程．
9．在产品质量检验时，常从产品中抽出一部分进行检查．现在从98件正品和2件次品共100件产品中，任意抽出3件检查．
（1）共有多少种不同的抽法？
（2）恰好有一件是次品的抽法有多少种？
（3）至少有一件是次品的抽法有多少种？
（4）恰好有一件是次品，再把抽出的3件产品放在展台上，排成一排进行对比展览，共有多少种不同的排法？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网