题目内容
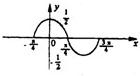 由图写出y=Asin(ωx+φ)的解析式,其中-π≤φ≤π.A>0,ω>0.
由图写出y=Asin(ωx+φ)的解析式,其中-π≤φ≤π.A>0,ω>0.
分析:先从图中得到A和T的值,然后根据周期的求法算出ω的值,最后根据特殊值确定φ得到解析式.
解答:解:由图可知A=
,T=π,∴ω=
=2
又因为当x=
时y=0代入可得:
sin(2×
+φ)=0∴
+φ=π+2kπ∴φ=
+2kπ
∵-π≤φ≤π∴φ=
∴解析式为:y=
sin(2x+
)
| 1 |
| 2 |
| 2π |
| π |
又因为当x=
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
∵-π≤φ≤π∴φ=
| π |
| 2 |
∴解析式为:y=
| 1 |
| 2 |
| π |
| 2 |
点评:本题主要考查根据三角函数的图象求三角函数解析式的问题.属基础题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<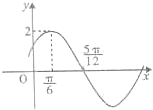 已知函数f(x)=Asin(ωx+φ),(A>0,ω<0,|φ|<
已知函数f(x)=Asin(ωx+φ),(A>0,ω<0,|φ|< )的表达式(A>0,ω>0,|
)的表达式(A>0,ω>0,|
