题目内容

1．将甲、乙、丙、丁四名大学生分配到三个不同的学校实习，每个学校至少分配一人，若甲、乙不能去同一个学校，则不同的分配方案共有（　　）
A．36种B．30种C．24种D．20种

分析 根据题意，用间接法分析：先求出将四名大学生分配到三个不同的学校，每个学校至少分到一名大学生的分配方法数目，再计算甲乙在一个学校的分配方法数目，然后用总的种数减去甲乙在一个学校的种数，即可得到答案．

解答 解：根据题意，先将4个大学生分成3组，有C42=6种分组方法，再将分好的3组全排列，分配到3个学校，有A33=6种情况，
计算将四名大学生分配到三个不同的学校，每个学校至少分到一名老师有C42•A33=36种分配方案，
若甲乙分配到同一个学校，在3个学校中选出1个，安排甲乙2人，有C31=3种情况，将剩余2人全排列，安排到其余2个学校，有A22=2种情况，
则甲乙分配到同一个学校的情况有3×2=6种分配方案；
则甲、乙不能去同一个学校的分配方案有36-6=30种；
故选：B．

点评 本题考查排列、组合的应用，直接分析涉及比较复杂的分类讨论，可以用间接法分析．

练习册系列答案
相关题目
11．设直l1，l2分别是函数f（x）=$\left\{\begin{array}{l}{-lnx，0＜x＜1}\\{lnx，x＞1}\end{array}\right.$图象上点P1，P2处的切线，l1与l2垂直相交于点P，且l1，l2分别与y轴相交于A，B，则△PAB的面积的取值范围是（　　）
A．（0，1）B．（1，+∞）C．（0，+∞）D．（0，2）
12．已知函数f（x）=cosxcos（x-$\frac{π}{6}$）+$\sqrt{3}$sin2x-$\frac{3\sqrt{3}}{4}$．
（1）求f（x）的最小正周期T；
（2）设g（x）=af（x）+b，若g（x）在[-$\frac{π}{4}$，$\frac{π}{4}$]上的值域为[0，3]，求实数a，b的值；
（3）若f（x）+1+（-1）n•m＞0对任意的x∈[-$\frac{π}{4}$，$\frac{π}{4}$]和n∈N*恒成立，求实数m的取值范围．
9．四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程和相关系数r，分别得到以下四个结论：
①y=2.35x-6.42，r=-0.93            ②y=-3.47x+5.65，r=-0.95
③y=5.43x+8.49，r=0.98            ④y=-4.32x-4.58，r=0.89
其中，一定不正确的结论序号是（　　）
A．②③B．①④C．①②③D．②③④
16．已知纯虚数z满足$\frac{1+2\overline{z}}{z}$=-2+i（其中i是虚数单位），则z=-i．
6．在△ABC中，角A，B，C所对的边分别为a，b，c，且$\frac{a}{cosA}=\frac{\sqrt{3}b}{sinB}$．
（Ⅰ）求角A的大小；
（Ⅱ）若a=2$\sqrt{3}$，B=$\frac{π}{4}$，求b．
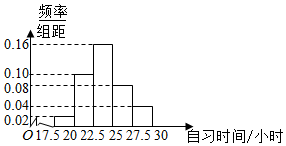13．某高校为调查1000名学生每周的自习时间（单位：小时），从中随机抽查了100名学生每周的自习时间，制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，估计这1000名学生中每周的自习时间不少于22.5小时的人数是700．
10．某单位在岗职工共有624人，为了调查工人用于上班途中的时间，该单位工会决定抽取10%的工人进行调查，请问如何采用系统抽样法完成这一抽样？
11．设函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）．若f（x）在区间（1，3）上具有单调性，且f（1）=-f（3）=-f（5），则ω=$\frac{π}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网