题目内容
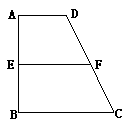
已知梯形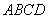 中,
中,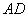 ∥
∥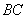 ,
,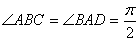 ,
, 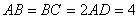 ,
,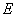 、
、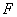 分别是
分别是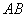 、
、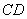 上的点,
上的点,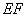 ∥
∥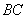 ,
,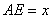 ,
, 是
是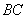 的中点.沿
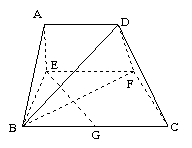
的中点.沿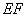 将梯形
将梯形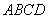 翻折,使平面
翻折,使平面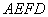 ⊥平面
⊥平面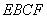 (如图) . (Ⅰ) 当
(如图) . (Ⅰ) 当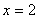 时,求证:
时,求证: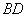 ⊥
⊥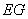 ;
;
(Ⅱ) 若以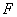 、
、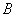 、
、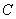 、
、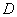 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为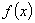 ,求
,求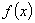 的最大值;
的最大值;
(Ⅲ)当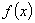 取得最大值时,求二面角
取得最大值时,求二面角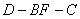 的余弦值.
的余弦值.
解:(Ⅰ)作 于
于 ,连
,连 ,
,
 由平面
由平面 平面
平面 知
知  平面
平面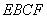
而 平面
平面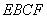 ,故
,故 又四边形
又四边形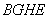
为正方形 ∴ 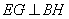
又 ,故
,故 平面
平面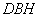
而 平面
平面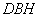 ∴
∴  .
.
(Ⅱ) ∵  ,面
,面 面
面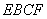 ∴
∴ 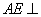 面
面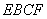
又由(Ⅰ) 平面
平面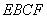 ∴
∴ 
所以 
 =
=




即 时
时 有最大值为
有最大值为 .
.
(Ⅲ)设平面 的法向量为
的法向量为
∵  ,
, ,
, ,
,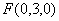 ∴
∴ 

则 即
即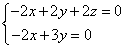 取
取  则
则 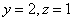 ∴
∴  面
面 的一个法向量为
的一个法向量为 则
则 <
< >
>
由于所求二面角 的平面角为钝角
的平面角为钝角
所以,此二面角的余弦值为-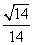 .
.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
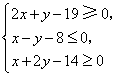 所表示的平面区域为
所表示的平面区域为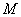 ,使函数
,使函数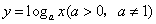 的图象过区域
的图象过区域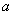 的取值范围是( )
的取值范围是( )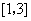 B.
B.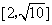 C.
C.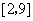 D.
D.
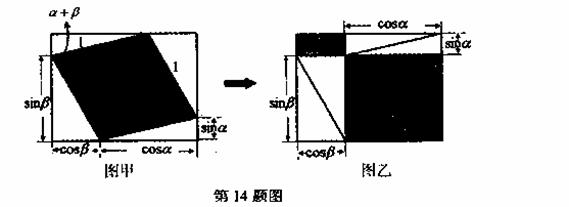
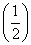 x,则f(1),g(0),g(-1)之间的大小关系是______________.
x,则f(1),g(0),g(-1)之间的大小关系是______________. 的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.
的图像与函数y=kx-2的图像恰有两个交点,则实数k的取值范围是________.